How to find Sector Area
Summary
TLDRIn this video, the speaker explains the concept of a sector area in geometry, focusing on how to calculate it using proportions. By comparing the sector area to the entire area of a circle, the speaker demonstrates the process step-by-step, highlighting the use of central angles and the formula πr² for the full area. The video covers the importance of proportions, cross-multiplying, and working with both degrees and radians. A practical example involving a 90-degree sector is also provided, with a clear explanation of how to solve the problem and round the answer correctly.
Takeaways
- 😀 A sector is a portion of a circle's area, not the entire area of the circle.
- 😀 To find the area of a sector, use the formula for the entire area of the circle (πr²) and apply proportions based on the central angle.
- 😀 The formula for sector area involves setting up a proportion: (central angle / 360) = (sector area / total area).
- 😀 Proportions are crucial for solving sector area problems, similar to how arc length is determined.
- 😀 The radius of the circle plays a key role in calculating the total area (πr²).
- 😀 When the central angle is 90°, the sector area is simply 1/4 of the total area of the circle.
- 😀 If the central angle is not 90°, use proportions to calculate the sector area by comparing the central angle to the full 360° of the circle.
- 😀 To solve for the unknown sector area, cross-multiply the proportions and solve for the sector area.
- 😀 In the example given, with a 90° angle, the sector area is calculated as 78.54 square units.
- 😀 If using radians, the central angle can be converted to degrees (π radians = 180°), and the same proportional method applies to find the sector area.
Q & A
What is a sector in a circle?
-A sector is a section of a circle, not the entire area of the circle, but a part of it that is formed by two radii and the intercepted arc.
How is the area of a sector related to the entire area of the circle?
-The area of a sector can be found using the proportional relationship between the central angle of the sector and the total angle of the circle (360 degrees). This is expressed as part/whole.
What formula is used to calculate the area of a full circle?
-The area of a full circle is calculated using the formula A = πr², where 'r' is the radius of the circle.
How can proportions be applied to find the area of a sector?
-Proportions can be applied by setting up a fraction where the central angle is over 360 degrees (the total angle of the circle), and the unknown sector area is over the total area of the circle.
What is the formula for finding the area of a sector given a central angle?
-The formula is (central angle / 360) * (πr²), where the central angle is in degrees and 'r' is the radius of the circle.
How do you solve for the area of the sector using the proportion method?
-To solve for the area of the sector, cross-multiply the proportion (central angle / 360 = sector area / full area), then solve for the unknown sector area.
What happens if the central angle is not 90 degrees?
-If the central angle is not 90 degrees, the proportion method still applies. You would simply use the actual central angle (e.g., 80 degrees, 100 degrees) in the formula instead of 90 degrees.
How is the area calculated when the central angle is 90 degrees?
-If the central angle is 90 degrees, the sector represents a quarter of the circle, and you can calculate the area by taking one-fourth of the total area of the circle (πr² / 4).
What are the steps involved in solving a sector area problem using proportions?
-1. Write the proportion (central angle / 360 = sector area / full area). 2. Cross-multiply the terms. 3. Solve for the sector area. 4. Round the answer as necessary based on the units (e.g., square units).
What is the difference between using degrees and radians in sector area calculations?
-When using radians, you need to convert the radians to degrees if they are not given directly in degrees. The conversion is that π radians equals 180 degrees. After converting, you can use the same proportion method to calculate the sector area.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Kesebangunan Segitiga: Kesebangunan Segitiga Siku-siku (Belajar Matematika Kelas 7) - Kak Hasan

Materi Matematika Kelas 8: Lingkaran

Cara Menghitung Panjang Busur dan Luas Juring Lingkaran
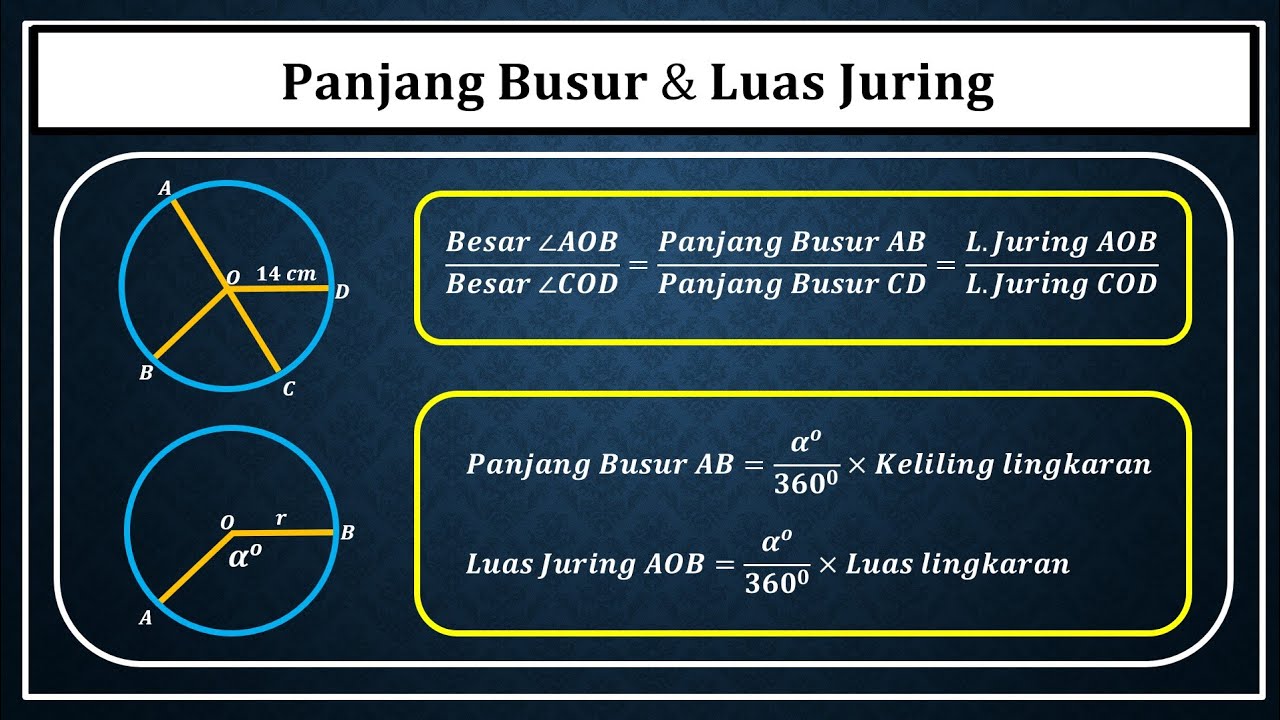
Panjang Busur dan Luas Juring Lingkaran

Bangun Ruang Sisi Lengkung [Part 3] - Bola
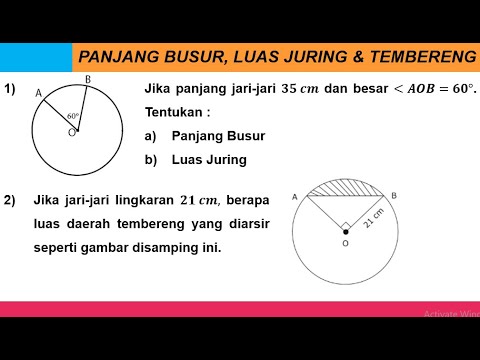
Cara Menghitung Panjang Busur, Luas Juring dan Luas Tembereng Pada Lingkaran
5.0 / 5 (0 votes)
