KELILING DAN LUAS SEGITIGA #MENEMUKAN RUMUS LUAS SEGITIGA#CONTOH SOAL#MATEMATIKA KELAS7
Summary
TLDRThis math lesson focuses on calculating the perimeter and area of triangles, including acute, right, and obtuse triangles. The video explains how to find the perimeter by summing the lengths of the sides and demonstrates the process for calculating the area using the base and height. Through step-by-step examples, viewers learn how to apply formulas to solve real-life problems. The video also covers the geometry of triangle heights and how they vary based on triangle type. Engaging examples reinforce the understanding of both perimeter and area, making the content accessible and informative.
Takeaways
- 😀 The perimeter of a triangle is the sum of the lengths of its three sides.
- 😀 To calculate the area of a triangle, you need the base (or one side) and the height (perpendicular distance from the base).
- 😀 The height of a triangle is the perpendicular line drawn from a vertex to the opposite side.
- 😀 Every triangle has three altitudes, one for each side considered as the base.
- 😀 In acute triangles, the altitudes are inside the triangle, while in obtuse triangles, some altitudes lie outside.
- 😀 The formula for the area of a triangle is: Area = 1/2 * base * height.
- 😀 For right-angled triangles, the area can also be calculated as 1/2 * base * height, where both the base and height are the legs of the triangle.
- 😀 The area of any triangle can be derived by comparing it to the area of a rectangle or parallelogram.
- 😀 The perimeter of a triangle is calculated by adding the lengths of all three sides.
- 😀 Example problem: The area and perimeter of a triangle can be calculated by applying formulas with given side lengths and heights, using the Pythagorean theorem for right triangles.
Q & A
What is the formula for the perimeter of a triangle?
-The perimeter of a triangle is the sum of the lengths of all three sides. It is calculated as: P = AB + BC + AC, where AB, BC, and AC are the side lengths.
How do you calculate the area of a triangle?
-The area of a triangle is calculated using the formula: Area = 1/2 * base * height, where 'base' is any side of the triangle, and 'height' is the perpendicular distance from the base to the opposite vertex.
What is the significance of the height in calculating the area of a triangle?
-The height is crucial because it is the perpendicular distance from the base to the top vertex of the triangle. It ensures that the area formula is based on the actual vertical space of the triangle.
What happens if the triangle is obtuse in terms of calculating height?
-In an obtuse triangle, the height may fall outside the triangle itself, as the height is defined as the perpendicular line from the vertex to the opposite side (or its extension).
How can we calculate the area of a right triangle?
-The area of a right triangle is calculated using the formula: Area = 1/2 * base * height. Since one of the angles is 90 degrees, the base and height are easily identifiable as the two legs of the triangle.
What is the relationship between the area of two congruent right triangles forming a rectangle?
-When two congruent right triangles are placed together, they form a rectangle. The area of the rectangle is equal to the sum of the areas of the two triangles, and each triangle's area is 1/2 * base * height.
In the example with triangle ABC, how is the perimeter calculated?
-To calculate the perimeter of triangle ABC, first find the length of BC using the Pythagorean theorem, then add up the lengths of sides AB, BC, and AC.
How does the formula for the area of a triangle change based on the type of triangle (acute, right, obtuse)?
-The formula for the area of a triangle remains the same regardless of its type: Area = 1/2 * base * height. The only difference is how the height is determined (whether inside or outside the triangle).
What are the key differences in height lines for acute, right, and obtuse triangles?
-In an acute triangle, all height lines fall inside the triangle. In a right triangle, the height corresponds to one of the legs. In an obtuse triangle, some height lines extend outside the triangle.
How do you solve for the area of a complex shape like quadrilateral PQRS in the transcript?
-The area of quadrilateral PQRS is solved by breaking it into triangles and calculating the areas of these smaller shapes, either by subtraction (for overlapping areas) or addition (for adjacent areas).
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Geometry – 7.1 Pythagorean Theorem and Its Converse

CLASSIFICATION OF TRIANGLES, according to their sides and according to their angles

Geometry 8-3: The Law of Sines

LEI DOS SENOS | TEOREMA DOS SENOS
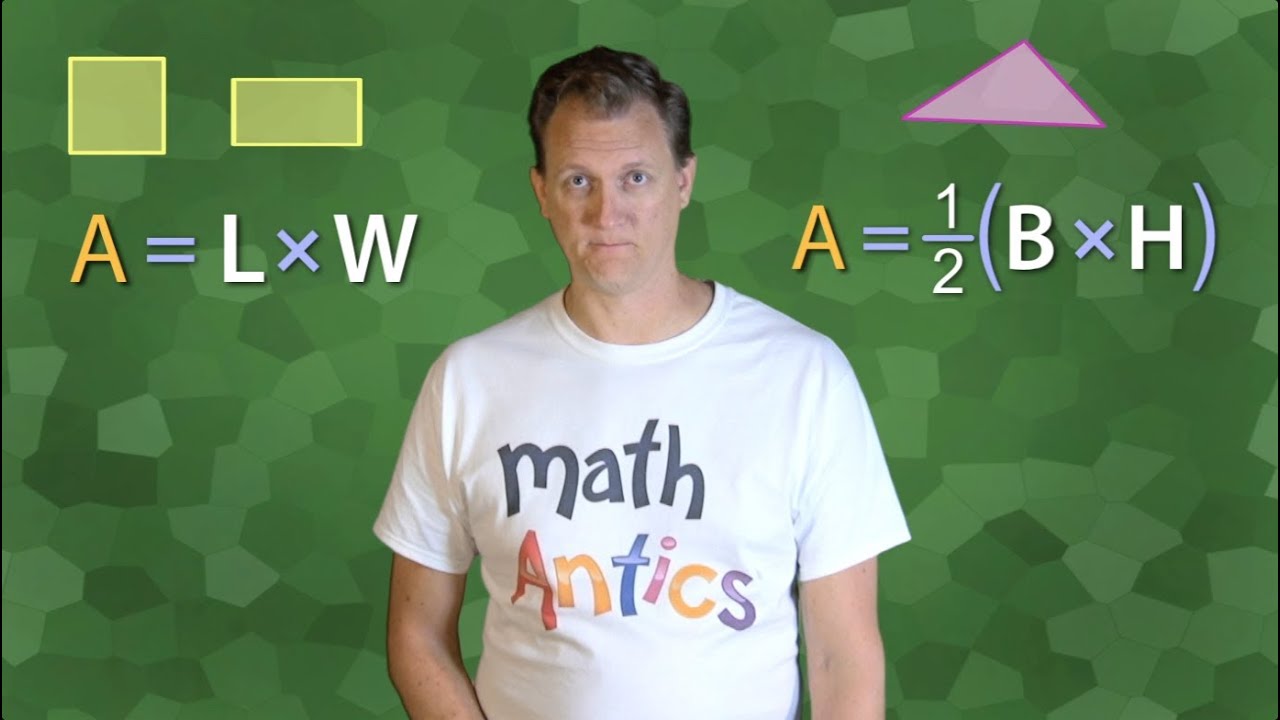
Math Antics - Area

Finding the Area of Oblique Triangles Using Heron's Formula | Grade 11 General Mathematics | Q3 W2
5.0 / 5 (0 votes)
