BENTUK AKAR DAN SIFAT-SIFATNYA - MATEMATIKA PEMINATAN KELAS X SMA

Summary

This video explains the concept of radical expressions and their properties in high school mathematics. The content covers the definition of radical forms, including square roots and cube roots, and their respective notations. Key properties of radicals, such as simplifying, multiplying, and dividing radicals, are thoroughly discussed with step-by-step examples. The video also includes solving problems involving radical expressions, showcasing how to apply these properties. It serves as an educational guide for students in class 10, aiming to simplify the topic and enhance understanding of radical expressions and their behavior.

Takeaways

• 😀 The lesson focuses on understanding the concept of square roots and nth roots in mathematics.
• 😀 A root is defined as a number 'B' such that when raised to the power 'n', it equals 'A'. This is written as B^n = A.
• 😀 The nth root of 'A' is denoted as √n(A), and the square root (n=2) can be written simply as √A, without the '2' exponent.
• 😀 Examples were provided for square roots and cube roots, such as √9 = 3 and ∛8 = 2.
• 😀 The first property of roots states that √n(A) * √n(B) = √n(A * B).
• 😀 An example demonstrating the first property: ∛3 * ∛9 = ∛27 = 3.
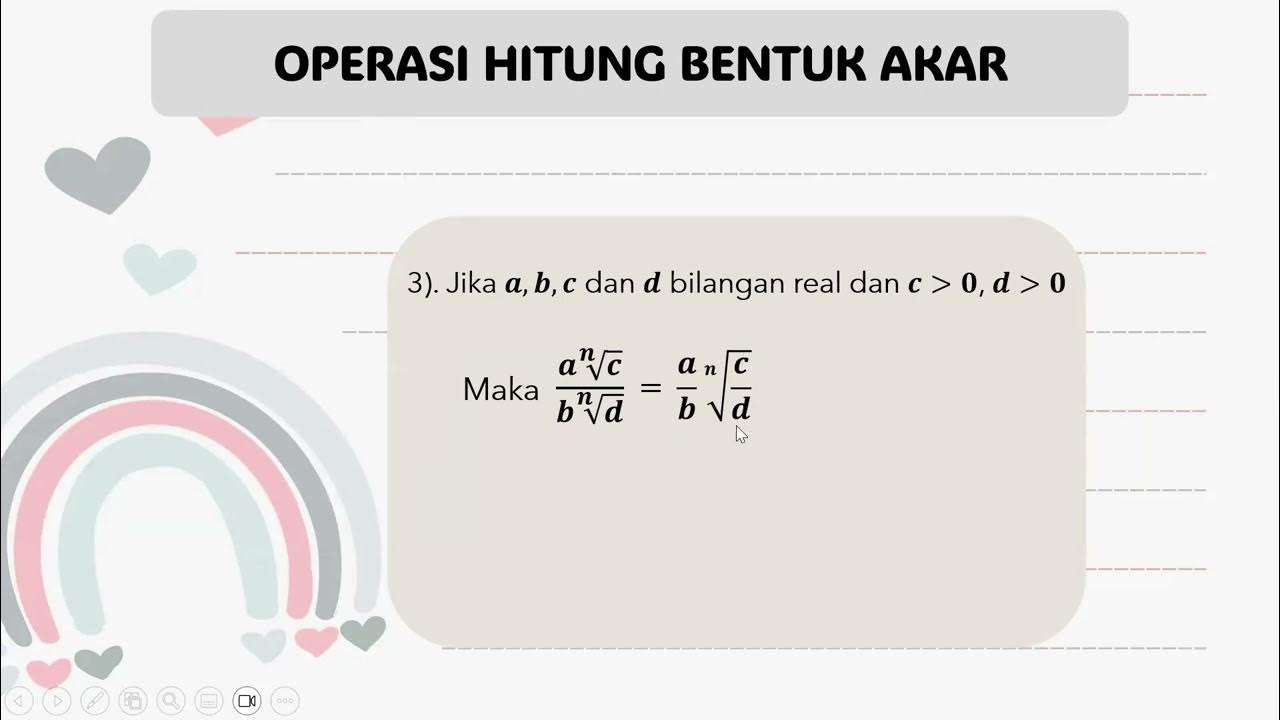
• 😀 The second property of roots is √n(A) / √n(B) = √n(A / B).
• 😀 An example demonstrating the second property: √96 / √6 = √16 = 4.
• 😀 The third property shows that √n(A) + √n(B) = (√n(A)) + (√n(B)) when the terms inside the roots are the same.
• 😀 The fourth property explains that √n(A^n) = A, which is useful for simplifying expressions involving powers and roots.
• 😀 The lesson also includes practice problems, such as simplifying expressions involving multiple roots, like 4√3 + 3√2 * 2√2 - 5√3.

Q & A

What is the definition of a radical expression in mathematics?

A radical expression involves the root of a number, denoted as the nth root of a number 'a'. In mathematical terms, if 'n' is a positive integer and 'B' is a real number, then 'B' raised to the power of 'n' equals 'a', and 'B' is the nth root of 'a'. This is written as the nth root of 'a'.

How do we simplify an expression with square roots, such as 3^2 = 9?

In the case of 3^2 = 9, the number 3 can be expressed as the square root of 9. For square roots, the index of the root (2) is typically not written, so it is simplified to '√9 = 3'.

What is the rule for multiplying two radical expressions with the same root?

When multiplying two radical expressions with the same root, such as the cube roots of 3 and 9, we multiply the numbers inside the radical and then take the root of the result. For example, '√3 * √9 = √27', which simplifies to 3.

How do you simplify a fraction under a radical, like √96 / √6?

To simplify a fraction under a radical, you divide the numbers inside the radical. For example, √96 / √6 simplifies to √(96/6) = √16, which equals 4.

What happens when you add or subtract two radical expressions with the same index and radicand?

When adding or subtracting radical expressions with the same root and radicand, you only combine the coefficients (numbers in front of the radical). For example, 3√7 + 6√7 equals 9√7.

How do you simplify expressions involving the addition and subtraction of radical terms with different radicands?

When dealing with radical terms with different radicands, you first simplify each term and then combine like terms. For example, 3√9 + 2√16 becomes 9 + 8, simplifying to 17.

What is the result when raising a radical expression to the same power as its index, like √(5^3)?

When raising a radical expression to the same power as its index, the radical and the exponent cancel each other out. For example, the cube root of 5^3 (³√(5^3)) equals 5.

How do you simplify expressions with powers and radicals, such as 4√x^4 y^4?

If you have a radical expression like 4√(x^4 y^4), you can simplify by taking the root of the terms inside the radical. In this case, the fourth root of x^4 and y^4 simplifies to x and y, so the result is x * y.

How do you multiply two radical expressions, like 2√50 and 3√32?

When multiplying radical expressions, you multiply the coefficients (numbers in front of the radical) and the terms inside the radical. For example, 2√50 * 3√32 becomes 6√(50 * 32) = 6√1600, which simplifies to 6 * 40 = 240.

How do you simplify the expression 4√3 + 3√2 * 2√2 - 5√3?

To simplify this expression, we apply the distributive property to the multiplication first, then combine like terms. Starting with 4√3 * 2√2 = 8√6, 3√2 * 2√2 = 6√2, and 4√3 * -5√3 = -20√3. Then, we add and subtract the like terms.