Kesebangunan - soal dan pembahasan materi kesebangunan matematika tingkat SMP kelas ix
Summary
TLDRIn this educational video from Matematika Hebat, the host discusses the concept of similarity in geometry, focusing on solving problems related to similar triangles. The video covers key concepts, such as proportionality of corresponding sides and congruence of angles. Through step-by-step examples, viewers learn how to calculate unknown side lengths in similar triangles using simple algebraic techniques. The host emphasizes the importance of identifying corresponding sides and applying proportionality rules to solve geometry problems. The video is designed to help students understand the topic better, especially for those in middle and high school levels.
Takeaways
- 😀 The video focuses on the concept of similarity in geometry, particularly for solving problems involving similar triangles.
- 😀 Two figures are considered similar if their corresponding sides have proportional lengths and their corresponding angles are congruent.
- 😀 The first condition for similarity is that the corresponding sides must have equal ratios (proportional sides).
- 😀 The second condition is that the corresponding angles of the two figures must be congruent (equal angles).
- 😀 Example 1 explains how to determine the missing side length in a pair of similar triangles using the proportionality rule.
- 😀 Cross-multiplication is used to solve for missing side lengths when dealing with similar figures and proportional sides.
- 😀 In Example 2, the speaker demonstrates solving for a missing side by setting up a proportion based on known values.
- 😀 Example 3 shows how to use a step-by-step approach to determine the unknown side length by analyzing corresponding sides and angles.
- 😀 The video emphasizes the importance of identifying corresponding sides and angles in similar figures to apply the proportionality rule effectively.
- 😀 At the end of the video, viewers are encouraged to send math problems for free assistance and are reminded to like, subscribe, and comment.
Q & A
What is the main topic discussed in the video?
-The main topic of the video is about the concept of similarity in geometry, specifically focusing on similar triangles and how to solve problems related to them.
What are the two conditions for two figures to be similar?
-The two conditions for two figures to be similar are: (1) the corresponding sides must be in equal ratios, and (2) the corresponding angles must be equal.
What is the first step when solving a problem involving similar triangles?
-The first step is to identify the corresponding sides between the two similar triangles.
How do you determine the length of an unknown side in similar triangles?
-To determine the length of an unknown side, you set up a proportion based on the corresponding sides of the similar triangles and solve for the unknown using cross multiplication.
In the first example, how do we calculate the length of side EF?
-To calculate the length of side EF, we use the proportion between the corresponding sides of the similar triangles, using the known values for sides AB, BC, and DF. The calculation is 15 * 6 / 12 = 7.5 cm.
What is the key principle used in solving the second example involving QR?
-The key principle is identifying corresponding sides, such as QR corresponding with PR, and then setting up a proportion to solve for the unknown side.
How does the method of cross-multiplication help in solving these problems?
-Cross-multiplication simplifies the process of solving proportions by allowing you to easily solve for the unknown by multiplying and dividing the known values.
What strategy is suggested for solving more complex problems like the one with EF?
-For more complex problems, the strategy involves drawing auxiliary lines, such as parallel lines, to break the problem into smaller parts and then using proportions to find the unknown side.
In the third example, how do we find the length of EF?
-In the third example, we use an auxiliary line to divide the larger triangle into smaller triangles, identify the corresponding sides, and apply the proportion method to find the length of EF.
What should you do if you are unsure about which sides are corresponding in similar triangles?
-If unsure about which sides are corresponding, you should carefully analyze the diagrams and identify the two triangles that are similar, then look for the sides and angles that are positioned in the same relative orientation.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Kurikulum Merdeka Materi Matematika Kelas 7 Bab 5 Kesebangunan

Kekongruenan dan Kesebangunan [Part 4] - Kesebangunan Dua Segitiga

KESEBANGUNAN BANGUN DATAR matematika SMP kelas VII Kurikulum Merdeka revisi 2022 Bab 5
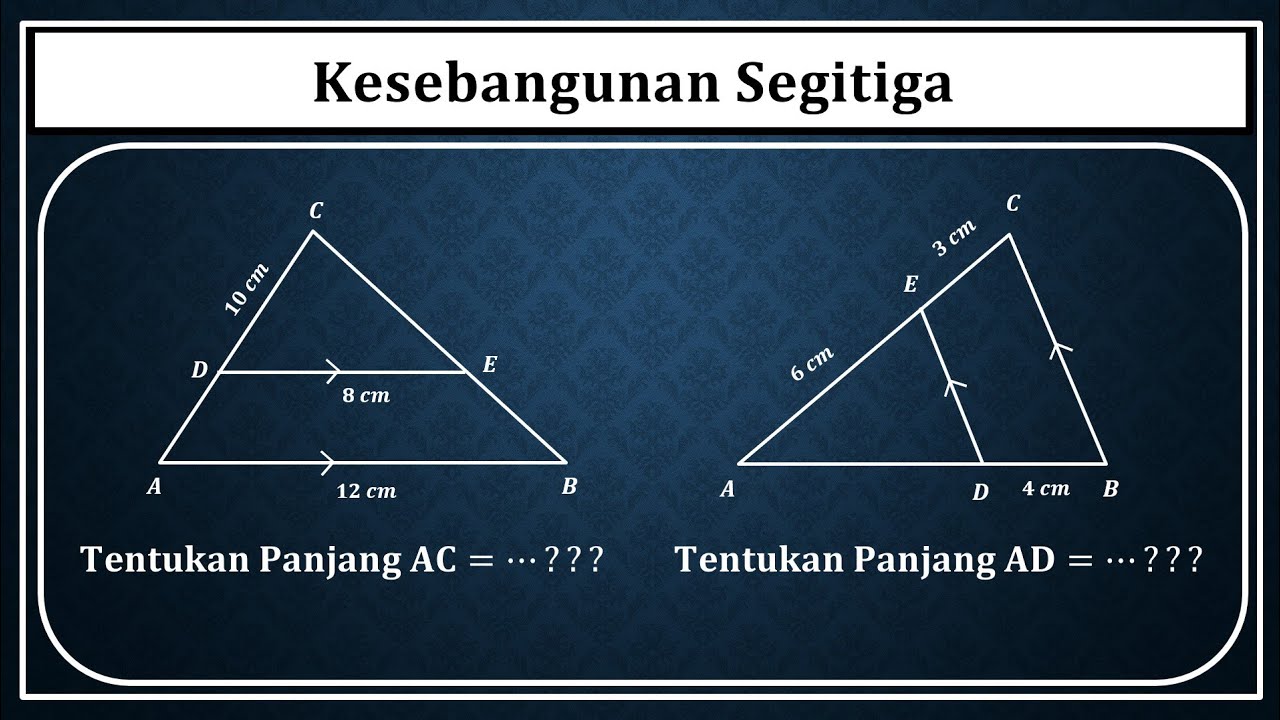
Kesebangunan segitiga

Kesebangunan Segitiga: Kesebangunan Segitiga Siku-siku (Belajar Matematika Kelas 7) - Kak Hasan

KESEBANGUNAN (Materi Kelas 9 SMP)
5.0 / 5 (0 votes)
