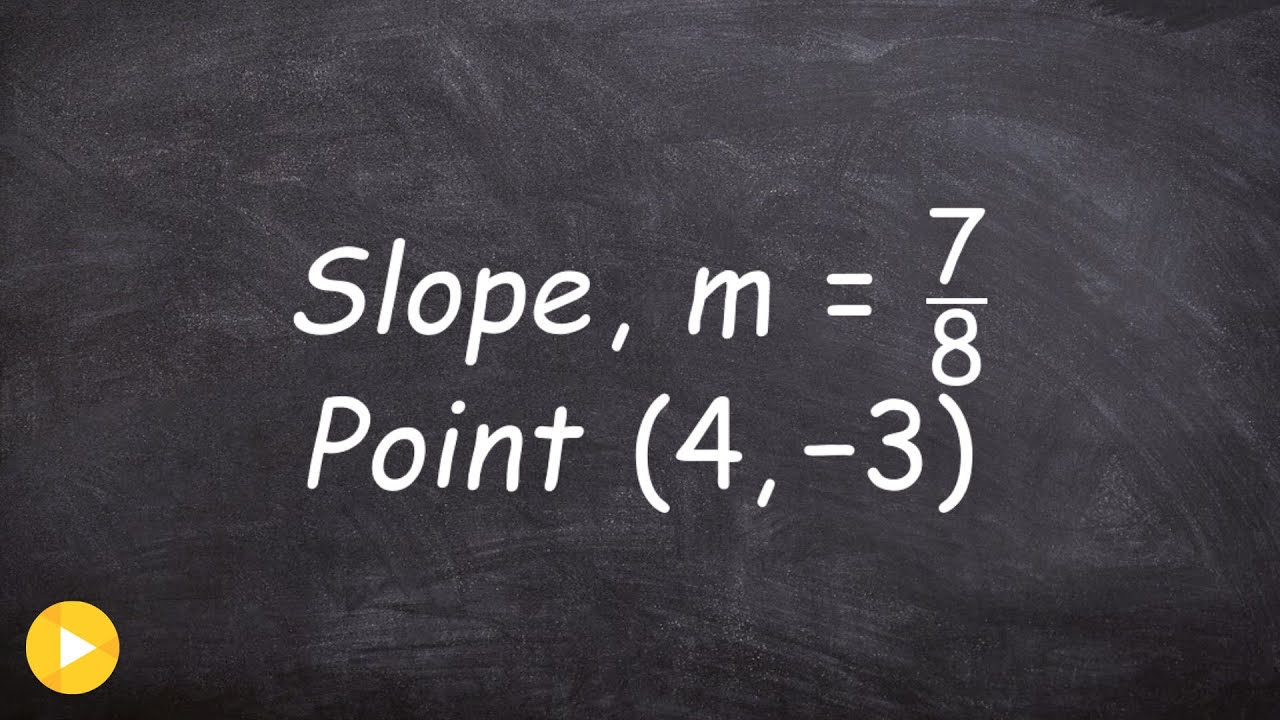Grade 8 Lesson 2.2: Point Slope Form Short Video
Summary
TLDRThis lesson explains different forms for writing the equation of a line, focusing on point-slope and slope-intercept forms. It covers the use of slope and points to find and write the equation, demonstrating how to work with a point and slope, two points, a table, and graphs. The video also highlights how to convert between point-slope form and slope-intercept form, and provides clear examples to reinforce understanding. Viewers are encouraged to practice with several examples to strengthen their grasp on writing and interpreting linear equations.
Takeaways
- 😀 The lesson focuses on understanding different forms of the equation of a line, specifically slope-intercept form and point-slope form.
- 😀 Slope-intercept form is useful when the slope (m) and the y-intercept (b) are known, and it simplifies the equation to y = mx + b.
- 😀 Point-slope form is used when a point (x1, y1) and the slope (m) are known, and it's written as y - y1 = m(x - x1).
- 😀 If given a point and slope, you can easily write the equation using point-slope form by substituting the values into the formula.
- 😀 When given two points, you can calculate the slope (m) using the formula (y2 - y1) / (x2 - x1) and then apply it to point-slope form.
- 😀 Tables with multiple points can be used to find a pair of points, and then you can follow the same steps as with two points to write the equation in point-slope form.
- 😀 For graphs, you can determine the slope by using the rise-over-run method, which involves counting vertical and horizontal distances between points on the line.
- 😀 To convert point-slope form to slope-intercept form, distribute the slope and simplify the equation to isolate y = mx + b.
- 😀 The lesson provides practice on using these forms in various scenarios, such as given points, a table, or a graph.
- 😀 When asked to graph an equation, first identify the point (x1, y1) from the equation, then use the slope to find additional points, and connect them to graph the line.
Q & A
What is the primary focus of the lesson in the script?
-The primary focus of the lesson is teaching different methods of writing the equation of a line, specifically using point-slope form and slope-intercept form.
What are the two key forms of equations discussed in the lesson?
-The two key forms discussed are the slope-intercept form (y = mx + b) and the point-slope form (y - y1 = m(x - x1)).
Why would someone prefer to use the point-slope form over the slope-intercept form?
-Point-slope form is preferred when you have a point (x1, y1) and a slope (m) and do not want to find the y-intercept (b).
What should you do if only two points are given, and you need to write the equation of the line in point-slope form?
-If only two points are given, first calculate the slope (m) using the formula (y2 - y1) / (x2 - x1), and then use the point-slope form with one of the points and the slope.
How can you calculate the slope if you are given a table of points?
-To calculate the slope from a table of points, select any two points and use the slope formula: m = (y2 - y1) / (x2 - x1).
What is the process to convert a point-slope form equation into the slope-intercept form?
-To convert from point-slope form to slope-intercept form, first distribute the slope (m) to the terms inside the parentheses, then isolate y to get the equation in the form y = mx + b.
What is the meaning of 'rise' and 'run' when calculating the slope?
-'Rise' refers to the vertical change (difference in y-values), and 'run' refers to the horizontal change (difference in x-values) between two points on the line.
How do you graph a line given the point-slope form of the equation?
-To graph a line from point-slope form, start at the point (x1, y1), then use the slope (rise/run) to find another point. Connect the points to graph the line.
What happens if you substitute 0 for x1 and y1 in the point-slope form?
-If you substitute 0 for both x1 and y1 in the point-slope form, the equation simplifies to the slope-intercept form, y = mx + b.
Why is it important to understand both the point-slope form and slope-intercept form?
-Understanding both forms allows for flexibility in solving problems, as some situations may give a point and slope (favoring point-slope form), while others may give the slope and y-intercept (favoring slope-intercept form).
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)