Pre-Calculus 12 - Video #25: Trigonometric Basics
Summary
TLDRThis video covers fundamental concepts of angles, including quadrant positioning, reference angles, and coterminal angles, focusing on their applications in trigonometry. It introduces radians and their relation to degrees, explaining arc length and how to calculate it. The video also explores practical examples, like finding the central angle of a circle given arc length and radius. With a focus on standard position, terminal arms, and circle rotation, the tutorial prepares viewers for more advanced scenarios involving angle conversions, arc length, and real-world problems such as clock mechanics.
Takeaways
- 😀 The Cartesian plane is divided into four quadrants, and the terminal arm rotates counterclockwise from the x-axis, affecting angle measurements.
- 😀 A terminal arm rotates counterclockwise, and angles in standard position are measured from the positive x-axis.
- 😀 Positive rotations (counterclockwise) are measured as positive angles, while negative rotations (clockwise) are negative angles, and they lead to coterminal angles.
- 😀 Coterminal angles have the same terminal arm position but differ by multiples of 360 degrees or 2π radians.
- 😀 Reference angles are acute angles formed between the terminal arm and the x-axis, and they are calculated differently depending on the quadrant.
- 😀 In quadrant 2, the reference angle is calculated as 180° minus the angle of rotation, while in quadrant 3, it's the angle minus 180°.
- 😀 In quadrant 4, the reference angle is calculated as 360° minus the angle of rotation.
- 😀 Coterminal angles help simplify negative angles into positive ones, making it easier to understand rotations and trigonometric calculations.
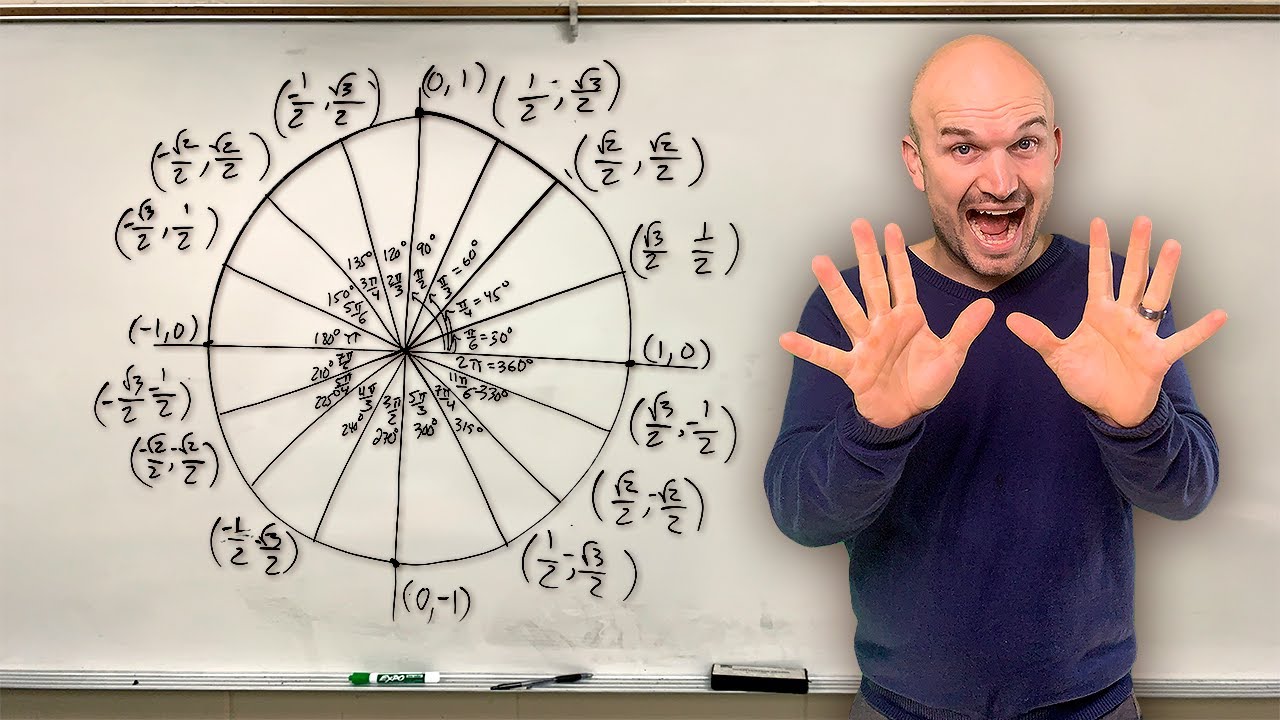
- 😀 The unit circle uses radians to measure angles, where one full rotation corresponds to 2π radians, or 360 degrees.
- 😀 To convert between degrees and radians, the ratio π/180 (or 180/π) is used depending on the desired unit.
- 😀 Arc length, the distance traveled by the terminal arm, can be calculated using the formula: Arc Length = radius × central angle (in radians).
Q & A
What is the purpose of the Cartesian plane in trigonometry?
-The Cartesian plane helps visualize angles and their rotation through four quadrants. It serves as a reference for plotting points and understanding the direction of rotations for trigonometric functions.
Why is the terminal arm in trigonometry rotated counterclockwise?
-The terminal arm rotates counterclockwise because the angle increases in that direction. The counterclockwise rotation is considered positive and is the standard for measuring angles in trigonometry.
What is the concept of 'standard position' in trigonometry?
-In standard position, the terminal arm of an angle originates from the origin of the Cartesian plane and initially lies along the positive x-axis. The angle is then measured by rotating the terminal arm counterclockwise.
What are coterminal angles?
-Coterminal angles are angles that have the same terminal arm, meaning they share the same position on the unit circle. These angles differ by full rotations (multiples of 360° or 2π radians).
How can you find the coterminal angle of -320°?
-To find a coterminal angle, you add 360° to the given negative angle. For -320°, adding 360° gives 40°, which is the positive coterminal angle.
What are reference angles, and how do you calculate them?
-Reference angles are acute angles formed between the terminal arm and the x-axis. To find the reference angle, subtract the given angle from 180° in the second quadrant, subtract it from 360° in the fourth quadrant, or subtract 180° from the angle in the third quadrant.
If an angle is 150°, how do you find its reference angle?
-To find the reference angle for 150°, subtract 150° from 180°, resulting in a reference angle of 30°.
How do you calculate the reference angle for 300°?
-For 300°, which is in the fourth quadrant, subtract 300° from 360°, giving a reference angle of 60°.
What is the relationship between degrees and radians?
-The relationship between degrees and radians is given by the ratio π radians = 180°. To convert from degrees to radians, multiply by π/180, and to convert from radians to degrees, multiply by 180/π.
How do you calculate the arc length of a circle with a known radius and central angle in radians?
-The formula for arc length is s = r × θ, where 'r' is the radius and 'θ' is the central angle in radians. If the angle is in degrees, convert it to radians first using the formula θ (radians) = θ (degrees) × π/180.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
Stop memorizing the unit circle
Materi Trigonometri

TRIGONOMETRI #3 (perbandingan trigonometri di berbagai kuadran)
Vektor Fisika • Part 1: Pengantar Trigonometri Dasar

Matematika SMA - Trigonometri (3) -Sistem Kuadran, Relasi Sudut Trigonometri (A)

Matematika SMA - Trigonometri (7) - Trigonometri Aturan Sinus dan Cosinus (A)
5.0 / 5 (0 votes)
