FISIKA KELAS XI - HUKUM BERNOULLI || FLUIDA DINAMIS

Summary

In this video, the concept of Bernoulli's Law is explored, which states that the sum of pressure, kinetic energy per unit volume, and potential energy per unit volume is constant along a streamline. Using a practical example involving water flow through pipes, the video demonstrates how Bernoulli's equation can be applied to calculate fluid velocity and pressure at different points. The video also highlights real-world applications of Bernoulli's Law, including its role in aircraft lift, fluid flow measurement devices like Venturimeters, and Pitot tubes. Viewers are encouraged to engage with the content through likes, shares, and subscriptions.

Takeaways

• 😀 Bernoulli's Principle states that the total energy (pressure energy, kinetic energy, and potential energy) at any point in a fluid remains constant along a streamline.
• 😀 The mathematical expression for Bernoulli's Principle is: P1 + (1/2) ρ v1² + ρ g h1 = P2 + (1/2) ρ v2² + ρ g h2.
• 😀 In fluid dynamics, Bernoulli's equation applies to incompressible, non-viscous fluids moving along a streamline.
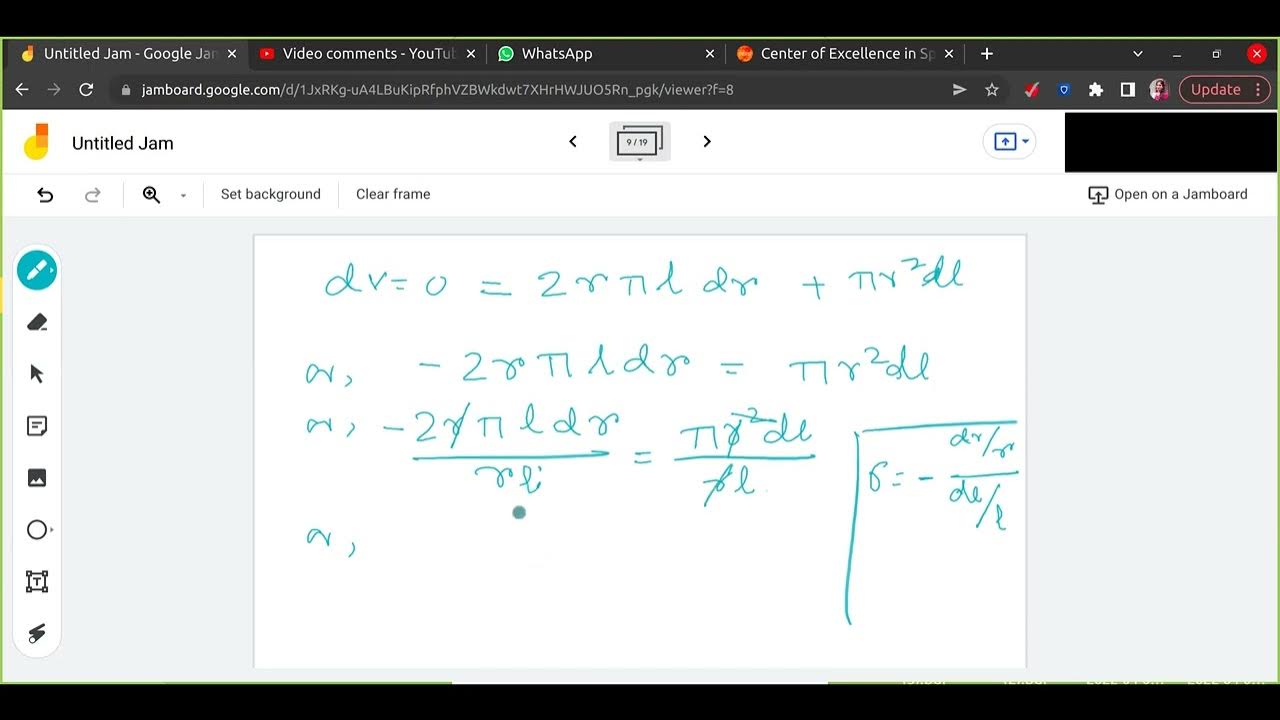
• 😀 The Continuity Equation is key for understanding fluid flow in pipes, where A1 v1 = A2 v2 relates the flow rates at different points in the pipe.
• 😀 In the example problem, Bernoulli’s Principle is used to calculate velocity and pressure at different points in a pipe with varying cross-sectional areas.
• 😀 The principle helps explain how pressure and velocity are inversely related in fluid flow: as velocity increases, pressure decreases, and vice versa.
• 😀 Bernoulli's equation can be used to solve real-life problems, such as determining the speed of water in pipes or measuring pressures in fluid systems.
• 😀 The script demonstrates solving a problem using given data like pipe cross-sectional areas, fluid velocity, and pressure to determine unknown values.
• 😀 Practical applications of Bernoulli's law include Venturimeters for measuring flow rates, Pitot tubes for measuring airspeed in aircraft, and the generation of lift in airplane wings.
• 😀 Bernoulli's law is also used to analyze fluid behavior in situations like tanks with leaks, which can be modeled using the principles discussed.

Q & A

What is Bernoulli's Law in fluid dynamics?

Bernoulli's Law states that the sum of pressure energy, kinetic energy, and potential energy per unit volume of a fluid remains constant along a streamline.

How is Bernoulli's Law mathematically expressed?

The equation for Bernoulli's Law is P1 + (1/2)ρV1² + ρgh1 = P2 + (1/2)ρV2² + ρgh2, where P is the pressure, ρ is the fluid density, V is the velocity, g is the acceleration due to gravity, and h is the height of the fluid.

What does each term in Bernoulli's equation represent?

In Bernoulli's equation: P is the pressure, ρ is the fluid density, V is the velocity, g is the gravitational acceleration (10 m/s²), and h is the height of the fluid relative to a reference point.

What is the significance of the principle in fluid flow through pipes?

In pipes with varying diameters and heights, Bernoulli’s principle explains how the pressure and velocity change as the fluid flows, ensuring energy conservation.

What example is used to explain Bernoulli’s principle in the video?

The video uses the example of water flowing through two connected sections of a pipe: one large and one small, with varying heights, to demonstrate how Bernoulli's principle applies.

How can the velocity of water in the small pipe be calculated?

Using the continuity equation, which states that A1V1 = A2V2 (where A is the cross-sectional area and V is the velocity), the velocity in the small pipe can be calculated by substituting the known values for the large pipe.

What formula is used to calculate the pressure in the small pipe?

The pressure in the small pipe is calculated using Bernoulli’s equation, taking into account the pressure, velocity, and height difference between the two points in the system.

What was the pressure value in the small pipe in the example?

Using the given values in the example, the pressure in the small pipe was found to be 200,000 Pa.

How does the height difference between the two pipes affect the pressure and velocity?

The height difference affects both pressure and velocity in the pipes; the pressure decreases as the velocity increases, maintaining the balance of energy as described by Bernoulli’s principle.

What real-life applications of Bernoulli's principle are mentioned in the video?

The video mentions several real-life applications, including the functioning of venturi meters, the operation of pitot tubes, and the lift generated by aircraft wings.