Varianza y Desviación Estándar - Ejercicio 2

Summary

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

Was ist die Formel für die Stichprobenvarianz?

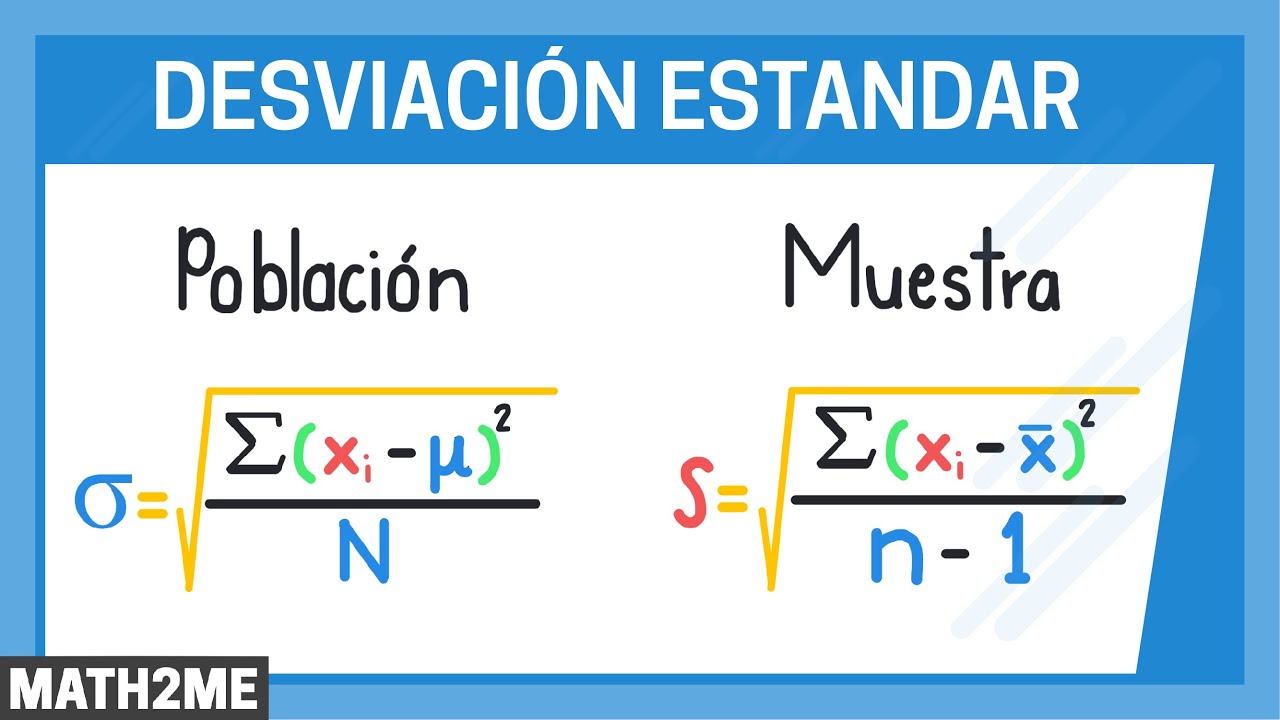
Die Formel für die Stichprobenvarianz lautet: s² = Σ(xi - x̄)² / (n - 1), wobei xi die einzelnen Beobachtungen, x̄ der Mittelwert der Stichprobe und n die Anzahl der Beobachtungen ist.

Wie berechnet man den Mittelwert einer Stichprobe?

Der Mittelwert einer Stichprobe wird berechnet, indem man alle Beobachtungen summiert und durch die Anzahl der Beobachtungen (n) teilt. Zum Beispiel: (12 + 20 + 16 + 18 + 19) / 5 = 17.

Warum muss man bei der Berechnung der Stichprobenvarianz n - 1 anstelle von n verwenden?

Die Verwendung von n - 1 anstelle von n dient der Korrektur für die Verzerrung, die entsteht, wenn man eine Stichprobe anstelle der gesamten Population verwendet. Dies wird als 'Bessel-Korrektur' bezeichnet und stellt sicher, dass die Varianz eine unverzerrte Schätzung der Populationsvarianz bleibt.

Wie berechnet man die Standardabweichung einer Stichprobe?

Die Standardabweichung einer Stichprobe wird berechnet, indem man die Quadratwurzel der Stichprobenvarianz zieht. Wenn die Varianz 10 beträgt, ist die Standardabweichung die Quadratwurzel von 10, was etwa 3,162 ergibt.

Warum ist es wichtig, die Symbole für Populations- und Stichprobenstatistiken zu verstehen?

Es ist wichtig, die Symbole für Populations- und Stichprobenstatistiken zu verstehen, weil sie in vielen Lehrbüchern und bei der Arbeit mit statistischen Formeln verwendet werden. Das Verständnis dieser Symbole hilft dabei, die richtigen Formeln anzuwenden und statistische Analysen korrekt zu interpretieren.

Was bedeutet es, wenn eine Varianz in Quadrat-Einheiten gemessen wird?

Wenn eine Varianz in Quadrat-Einheiten gemessen wird, bedeutet dies, dass die Einheiten der Originaldaten quadriert wurden. Zum Beispiel, wenn die Originaldaten in Dollar sind, wird die Varianz in 'Dollar²' angegeben.

Welche Schritte sind notwendig, um die Varianz einer Stichprobe zu berechnen?

Um die Varianz einer Stichprobe zu berechnen, subtrahiert man den Mittelwert jeder Beobachtung, quadriert das Ergebnis, summiert alle quadrierten Abweichungen und teilt die Summe durch (n - 1).

Was ist der Unterschied zwischen der Varianz einer Population und der Varianz einer Stichprobe?

Der Unterschied liegt in der Anzahl der Elemente, die verwendet werden, um die Berechnung vorzunehmen. Bei der Population wird die Varianz durch n geteilt, während bei der Stichprobe (n - 1) verwendet wird, um eine verzerrungsfreie Schätzung zu erhalten.

Warum wird die Varianz einer Stichprobe durch n - 1 anstatt durch n geteilt?

Die Varianz einer Stichprobe wird durch n - 1 geteilt, um die Verzerrung zu korrigieren, die bei der Schätzung der Populationsvarianz durch eine Stichprobe entsteht. Dies sorgt dafür, dass die Stichprobenvarianz eine genauere Schätzung der wahren Populationsvarianz liefert.

Welche Symbole werden für den Mittelwert, die Varianz und die Standardabweichung in der Population und der Stichprobe verwendet?

Für die Population werden die Symbole μ (Mittelwert), σ² (Varianz) und σ (Standardabweichung) verwendet. Für die Stichprobe verwendet man die Symbole x̄ (Mittelwert), s² (Varianz) und s (Standardabweichung).