MEDIDAS DE DISPERSION PARA DATOS AGRUPADOS
Summary
TLDREn este video, se resuelve un ejercicio de estadística con datos agrupados. El proceso incluye calcular la media aritmética, el rango, la desviación media, la varianza y la desviación típica o estándar. El ejercicio comienza con la organización de los datos en intervalos y frecuencias, seguido del cálculo de marcas de clase, la multiplicación de estas por las frecuencias, y la sumatoria de los resultados. Luego se utilizan fórmulas específicas para encontrar los valores solicitados, finalizando con la desviación típica, demostrando cómo abordar estos cálculos paso a paso en datos agrupados.
Takeaways
- 😀 El ejercicio se basa en calcular estadísticas con datos agrupados, como la media aritmética, el rango, la desviación media, la varianza y la desviación estándar.
- 😀 Se realizó una encuesta sobre los pagos por consumo de agua potable, con datos agrupados en intervalos de clase y frecuencias absolutas.
- 😀 Los intervalos de clase corresponden a los rangos de pago: entre 10-20, 20-30, 30-40, 40-50, 50-60, y 60-70 dólares.
- 😀 La marca de clase se calcula sumando los límites superior e inferior del intervalo y dividiendo entre 2.
- 😀 Para obtener la media aritmética, se multiplican las marcas de clase por sus respectivas frecuencias y se dividen entre el número total de encuestados.
- 😀 El rango se calcula restando el valor máximo del valor mínimo de los intervalos, en este caso 70 - 10 = 60.
- 😀 La desviación media se obtiene sumando los valores absolutos de las diferencias entre las marcas de clase y la media aritmética, multiplicados por la frecuencia, y dividiendo entre el número total de encuestados.
- 😀 Para calcular la varianza, se elevan al cuadrado las diferencias entre la marca de clase y la media aritmética, luego se multiplican por la frecuencia y se dividen por el número total de encuestados.
- 😀 La desviación estándar o típica se obtiene al calcular la raíz cuadrada de la varianza.
- 😀 En resumen, el proceso involucra organizar los datos en una tabla, aplicar fórmulas estadísticas y calcular varios indicadores para describir los datos del ejercicio.
Q & A
¿Qué medidas estadísticas se deben calcular en el ejercicio?
-Las medidas estadísticas que se deben calcular en este ejercicio son: la media aritmética, el rango, la desviación media, la varianza y la desviación típica o estándar.
¿Cómo se determinan los intervalos de clase en el ejercicio?
-Los intervalos de clase se proporcionan directamente en el ejercicio. En este caso, son rangos de pago de consumo de agua potable, como 10-20, 20-30, etc.
¿Qué significa la columna 'marca de clase' y cómo se calcula?
-La 'marca de clase' es el punto medio de cada intervalo de clase. Se calcula sumando el límite inferior y el límite superior del intervalo y dividiendo el resultado entre dos.
¿Qué fórmula se utiliza para calcular la media aritmética?
-La fórmula para calcular la media aritmética es la suma de los productos de cada marca de clase por su frecuencia absoluta, dividida por el total de los datos (frecuencia total).
¿Cómo se calcula el rango de los datos?
-El rango se calcula restando el valor máximo del valor mínimo de los datos. En este caso, es la diferencia entre el valor mayor (70) y el valor menor (10).
¿Qué es la desviación media y cómo se calcula?
-La desviación media mide el promedio de las diferencias absolutas entre los valores de las marcas de clase y la media aritmética. Se calcula multiplicando estas diferencias absolutas por las frecuencias correspondientes, sumando los resultados y dividiendo entre el total de los datos.
¿Cómo se calcula la varianza de los datos?
-La varianza se calcula elevando al cuadrado la diferencia entre cada marca de clase y la media aritmética, multiplicando por la frecuencia absoluta, sumando estos productos y dividiendo entre el total de los datos.
¿Qué fórmula se utiliza para calcular la desviación estándar?
-La desviación estándar se calcula tomando la raíz cuadrada de la varianza obtenida previamente.
¿Por qué es importante obtener la frecuencia total antes de calcular la media y otras medidas?
-Es importante obtener la frecuencia total porque este valor es el denominador en las fórmulas para calcular la media, la desviación media, la varianza y la desviación estándar. Asegura que las sumas y promedios se realicen correctamente.
¿Cómo se maneja el signo negativo al calcular las diferencias absolutas?
-Cuando se calculan las diferencias entre la marca de clase y la media aritmética, si el resultado es negativo, se toma su valor absoluto. Esto garantiza que todas las desviaciones sean positivas, independientemente de si el valor original era mayor o menor que la media.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Cómo calcular las medidas de tendencia central para datos agrupados

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS

Media mediana y moda | Datos sin agrupar
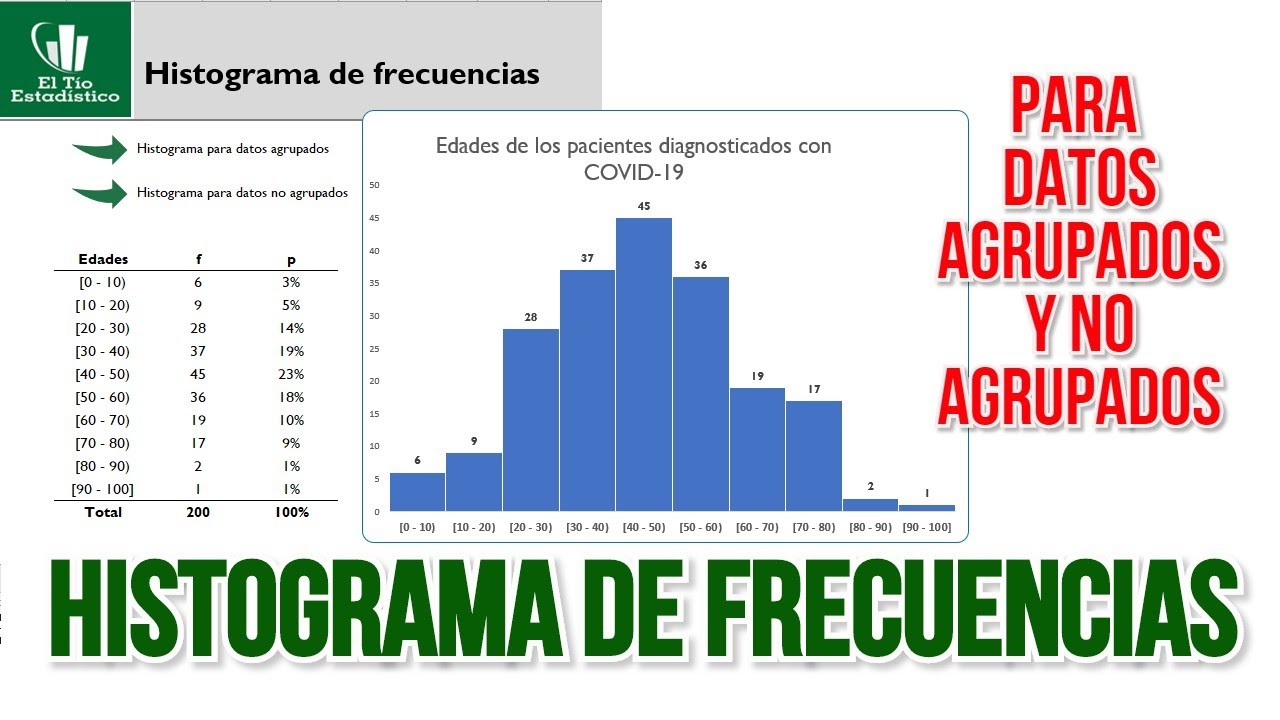
Cómo hacer un histograma de frecuencias en Excel ✅ | Estadística Descriptiva ⭐

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición

Calcular MEDIA, MEDIANA y MODA. Datos agrupados y no agrupados.
5.0 / 5 (0 votes)
