METODE NUMERIK 11 REGRESI LINIER

Summary

This video explains linear regression and numerical methods, focusing on the process of fitting a function to data through numerical differentiation and least squares minimization. It highlights the difference between regression and correlation, explaining how regression models the cause-and-effect relationship between variables. The tutorial includes practical examples, explaining how to calculate coefficients (a and b) for the regression line using different methods, and how to use the model to predict outcomes. Additionally, the video introduces concepts like the coefficient of determination (R-squared) and standard deviation of errors, providing insight into how accurately the regression model fits the data.

Takeaways

• 😀 Regression analysis helps in understanding the relationship between variables, with the goal of predicting or estimating one variable based on the value of another.
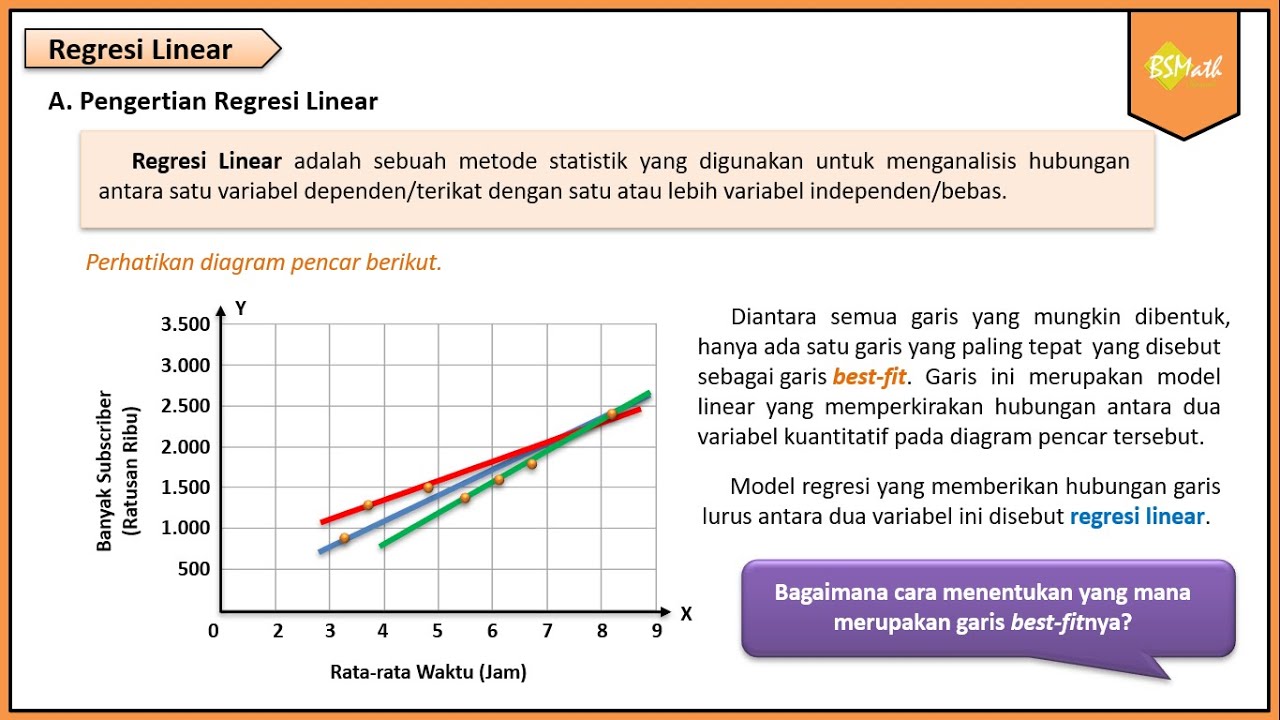
• 😀 Linear regression is a method that involves fitting a linear equation (Y = a + bX) to the data points, where 'a' is the intercept and 'b' is the regression coefficient.
• 😀 The key difference between regression and correlation is that regression examines the magnitude of the effect between variables, while correlation measures the strength of the relationship without implying causality.
• 😀 Regression analysis is typically used when one variable is dependent (Y) and the other is independent (X), allowing prediction of Y from X.
• 😀 In regression, the goal is to minimize the error (residuals) between the predicted and observed values using methods like least squares.
• 😀 The coefficient of determination (R²) explains how well the regression model fits the data, with values closer to 1 indicating a better fit.
• 😀 A high R² value (e.g., 0.6696) means that a large proportion of the variation in the dependent variable (Y) is explained by the independent variable (X).
• 😀 The standard deviation of the residuals measures the accuracy of predictions made by the regression model, indicating how well the model approximates the data.
• 😀 The script explains how to calculate the regression coefficients (a and b) using summations of the data points, such as ΣX, ΣY, ΣX², and ΣXY.
• 😀 An example is provided where the regression analysis is applied to data on work experience (X) and sales revenue (Y) to predict future sales based on experience.
• 😀 The script also demonstrates how to calculate predictions for specific values of X (such as work experience) and provides formulas to compute the regression equation, R², and standard deviation.

Q & A

What is the main objective of using numerical methods in regression analysis?

The main objective is to numerically calculate the derivative of a function and to solve differential equations, especially when empirical data or measured values are involved, which may contain random errors or stochastic behavior.

What is the difference between regression and correlation?

Regression analyzes the impact of one variable on another (causal relationship), while correlation analyzes the degree of association between variables without implying causality. Additionally, regression requires both independent and dependent variables, whereas correlation does not.

What does linear regression help to determine?

Linear regression helps determine the relationship between two variables, allowing predictions of the dependent variable (Y) based on the independent variable (X). It is used to fit a straight line through the data points and estimate unknown values.

What is the formula for a simple linear regression model?

The formula for a simple linear regression model is: Y = a + bX, where 'Y' is the dependent variable, 'a' is the intercept (constant), 'b' is the regression coefficient (slope), and 'X' is the independent variable.

How do you calculate the regression coefficients 'a' and 'b' in linear regression?

The regression coefficients 'a' (intercept) and 'b' (slope) can be calculated using summation formulas that involve the values of X and Y. Specifically, 'a' is calculated using the formula: a = (ΣY * ΣX^2 - ΣX * ΣXY) / (n * ΣX^2 - ΣX^2), and 'b' is calculated using: b = (ΣXY - ΣX * ΣY) / (n * ΣX^2 - ΣX^2).

What is the significance of the coefficient of determination (R-squared) in regression analysis?

R-squared (R²) measures how well the regression model fits the data. It represents the proportion of the variance in the dependent variable that can be explained by the independent variable(s). A higher R-squared indicates a better fit.

How do you interpret an R-squared value of 0.6696?

An R-squared value of 0.6696 means that approximately 66.96% of the variance in the dependent variable (sales) is explained by the independent variable (experience). The remaining 33.04% of the variance is due to other factors not included in the model.

What does the standard error of estimate (or standard deviation) tell us in regression analysis?

The standard error of estimate measures the accuracy of the predictions made by the regression model. It reflects how much the actual data points deviate from the predicted values. A smaller standard error indicates a more accurate model.

What is the practical application of linear regression in real-life scenarios?

Linear regression is widely used in forecasting and predicting outcomes based on known data. For example, it can be used to predict sales based on years of experience, estimate property prices based on location and size, or evaluate the impact of one factor on another in scientific research.

In the provided example, how was the regression equation used to predict sales for a worker with 3.5 years of experience?

In the example, the regression equation was Y = 3.25 + 1.25X. By substituting X = 3.5 (years of experience), the equation predicted that the sales would be Y = 3.25 + 1.25 * 3.5 = 7.625.