Rotasi Terhadap Titik Pusat O(0,0) - Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka
Summary
TLDRThis video explains the concept of rotation (rotasi) in geometry for high school students, focusing on the rotation of points around a central origin (0,0). The speaker breaks down the process of rotating a point by a given angle, using positive angles for counterclockwise and negative angles for clockwise rotation. The session explores rotation formulas, including the use of transformation matrices, and provides a practical example of rotating a point by 270°. By the end, viewers gain a solid understanding of rotation in geometry, reinforced with practice problems to ensure comprehension.
Takeaways
- 😀 Rotations in geometry are transformations that move points by rotating them around a specific center by a given angle (alpha).
- 😀 A positive angle results in a counterclockwise rotation, while a negative angle results in a clockwise rotation.
- 😀 A full rotation equals 360 degrees, with commonly used angles being 0°, 90°, 180°, and 270° for transformations.
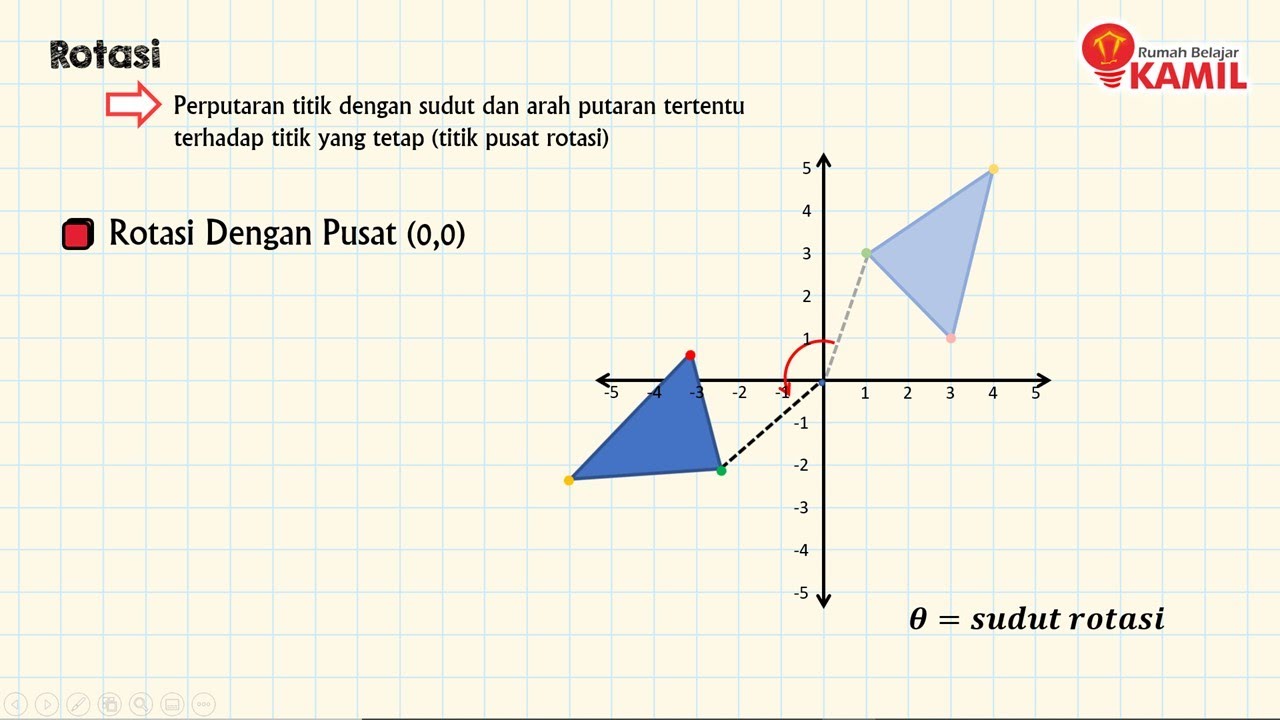
- 😀 To perform a rotation, especially on a coordinate plane, it's crucial to first understand how to rotate a point with respect to a given center, typically (0,0).
- 😀 The rotation of a point involves determining how its coordinates change as it is rotated around the center by a specific angle.
- 😀 For a 90-degree rotation counterclockwise around the origin (0,0), the new coordinates of a point (x, y) will be (-y, x).
- 😀 Rotation transformations can be described using a transformation matrix that allows for easy calculation of new coordinates.
- 😀 To rotate a point by an arbitrary angle alpha, the general matrix formula is: [[cos(α), -sin(α)], [sin(α), cos(α)]] applied to the point's coordinates (x, y).
- 😀 Example: A rotation by 270° around the origin would transform a point (x, y) based on a transformation matrix for cos(270°) and sin(270°).
- 😀 Practice problems can include finding the coordinates of an original point given its rotated image, reinforcing the application of rotation matrices.
- 😀 It is essential to memorize trigonometric values for common angles (e.g., 30°, 45°, 90°, etc.) to perform rotations efficiently.
Q & A
What is the main topic discussed in the video?
-The video focuses on geometric transformations, specifically rotation (or perputaran), and explains how rotation works in geometry for high school level mathematics.
What is rotation in geometric transformations?
-Rotation is a transformation that moves points by rotating them around a specific center point by a given angle, either counterclockwise or clockwise, depending on whether the angle is positive or negative.
How does a positive angle affect the direction of rotation?
-A positive angle causes the rotation to occur counterclockwise, i.e., in the opposite direction of the clock's hands.
What happens when the angle is negative during a rotation?
-A negative angle results in a clockwise rotation, i.e., the rotation follows the direction of the clock's hands.
How do you represent a rotation of 90 degrees on a Cartesian coordinate system?
-In a Cartesian coordinate system, a 90-degree rotation counterclockwise transforms a point (x, y) to (-y, x).
What formula is used for rotating a point by 90 degrees counterclockwise around the origin?
-The general formula for a 90-degree counterclockwise rotation around the origin is: (x, y) -> (-y, x).
What is the significance of the transformation matrix for rotation?
-The transformation matrix for rotation expresses the relationship between the coordinates of the original point and the coordinates of the rotated point. It is used to compute rotations at any angle.
How can you perform a rotation using a matrix transformation?
-To perform a rotation using a matrix, you multiply the point's coordinates by the appropriate rotation matrix for the given angle. For example, for an angle of alpha, the matrix is: [cos(alpha) -sin(alpha); sin(alpha) cos(alpha)].
What is the transformation matrix for a 270-degree rotation?
-The transformation matrix for a 270-degree rotation is: [0 1; -1 0]. This matrix is used to rotate points counterclockwise by 270 degrees.
How do you calculate the coordinates of a point rotated 270 degrees around the origin?
-To calculate the coordinates of a point rotated by 270 degrees, use the formula: (x, y) -> (y, -x). This involves using the transformation matrix [0 1; -1 0] and applying it to the point's coordinates.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Transformasi Geometri Bagian 3 - Rotasi (Putaran) Matematika Wajib Kelas 11
Matematika kelas 9 : Transformasi Geometri (part 3 : Rotasi I)

Transformasi Geometri [Part 3] - Rotasi (Perputaran)

ROTASI (Perputaran) - Cara menentukan bayangan titik di pusat (0,0) dan (a,b)

ROTASI (PERPUTARAN) || TRANSFORMASI GEOMETRI

Understanding the Rotation Matrix
5.0 / 5 (0 votes)
