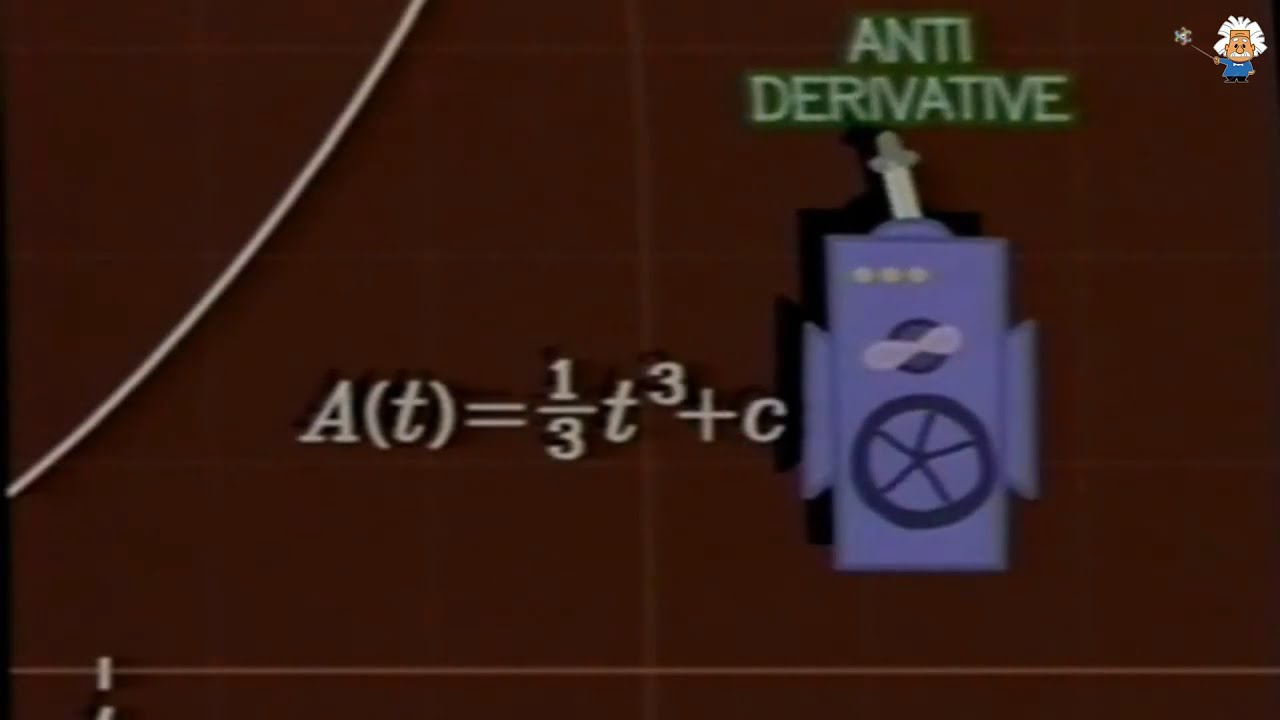Birth of Calculus (Part 1)
Summary
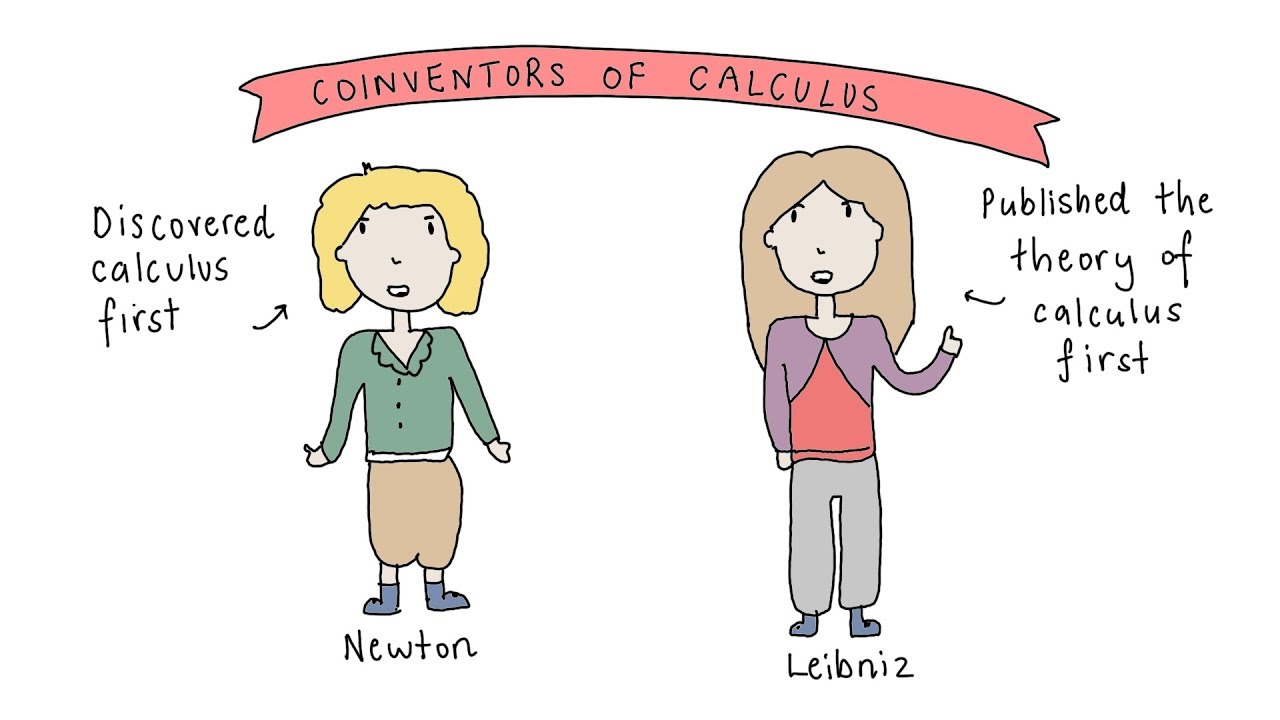
TLDRThis video explores the pivotal discoveries of calculus by Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century. It delves into Newton's early work at Cambridge, highlighting his mastery of tangent and area problems through innovative methods, including his examination of mechanical curves. Newton's systematic approach and insights into the relationship between motion and calculus laid the groundwork for future mathematical theories. The preserved notebooks of both mathematicians offer a fascinating glimpse into their thought processes and the evolution of their groundbreaking ideas.
Takeaways
- 😀 Isaac Newton and Gottfried Wilhelm Leibniz independently discovered calculus, with Newton's work beginning around 1665.
- 😀 Original writings of both mathematicians are preserved in libraries, providing insight into their discovery processes.
- 😀 Newton studied mathematics intensely during his time at Trinity College, Cambridge, where he developed fundamental ideas on calculus.
- 😀 He improved upon contemporary methods for finding tangents to polynomial curves, specifically through geometric constructions.
- 😀 Newton's 'waste book' documented his various mathematical discoveries, including methods for finding normals and tangents.
- 😀 By the summer of 1665, Newton had established relationships between tangent problems and area problems.
- 😀 His exploration of mechanical curves, particularly the cycloid, advanced his understanding of motion and tangents.
- 😀 Newton's innovative method involved analyzing the ratio of velocities of points moving along a curve to find tangents.
- 😀 In November 1665, he developed a general method for drawing tangents to curves, marking a significant step in calculus.
- 😀 Despite his advancements, Newton's methods remained mathematically imprecise until further developments were made.
Q & A
Who are the two men credited with the invention of calculus?
-Isaac Newton and Gottfried Wilhelm Leibniz are both credited with the invention of calculus.
When did Isaac Newton first discover calculus?
-Isaac Newton discovered calculus around 1665 or 1666.
What is the significance of the original writings of Newton and Leibniz?
-Their original writings provide a fascinating glimpse into their mathematical discovery processes and are preserved in the University Library in Cambridge.
What were Newton's initial mathematical studies focused on during 1665?
-Newton focused on mastering methods for finding tangents to polynomial curves, as well as exploring concepts in optics and gravitation.
What method did Newton develop for finding tangents to curves?
-Newton developed a method that involved calculating the ratio of velocities of points moving along the x and y axes, which helped him determine the direction of the tangent.
What is a cycloid and how is it relevant to Newton's work?
-A cycloid is the path traced by a point on the circumference of a rolling circle, and Newton studied it to understand the instantaneous direction of motion along curves.
How did Newton's approach to tangents differ from previous methods?
-Newton's approach was more general and systematic, allowing him to find tangents to all curves without relying on the complicated calculations used by earlier mathematicians like Huygens.
What was Newton's breakthrough regarding mechanical curves?
-Newton's breakthrough was recognizing that he could define curves through motion and relate velocities of two moving points, leading to a general method for drawing tangents.
What did Newton conclude about the relationship between tangent problems and area problems?
-Newton understood that tangent problems and area problems are inversely related; solving one would help in solving the other.
Why is the date November 13, 1665, significant in the context of Newton's discoveries?
-On this date, Newton developed a new method for finding tangents that marked a significant step in the development of calculus, asserting that it could apply to all curves.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)