Determining angle of rotation
Summary
TLDRThis instructional video explores the concept of rotation in geometry, specifically how to determine the angle of rotation for geometric shapes. Through two examples—a triangle and a quadrilateral—the instructor demonstrates the process of identifying rotation angles by analyzing the movement of specific points. The first example reveals a 60-degree counterclockwise rotation for triangle ABC to A'B'C', while the second shows a negative 90-degree clockwise rotation for quadrilateral ABCD to A'B'C'D'. The video emphasizes visual assessment and familiar angle comparisons to facilitate understanding.
Takeaways
- 😀 The video explains how to determine the angle of rotation for triangles and quadrilaterals under rotation around a point.
- 🔄 Triangle A'B'C' is the image of triangle ABC after rotation about the origin.
- 🔍 Visual inspection is key: analyze the movement of points from their original position to their new position.
- ➡️ For triangle A to A', the counterclockwise rotation suggests a positive angle.
- 📏 The instructor determines the angle of rotation as 60 degrees, noting it is two-thirds of a right angle.
- 🟡 Quadrilateral A'B'C'D' is shown as the image of quadrilateral ABCD under rotation about point Q.
- ⏱️ The movement from B to B' involves a clockwise rotation, indicating a negative angle.
- 🔺 The instructor concludes the angle of rotation for the quadrilateral is negative 90 degrees.
- ✏️ Each point’s rotation is assessed to verify that all points align with the calculated angle.
- 🤔 Viewers are encouraged to pause and apply the reasoning to confirm their understanding of rotation angles.
Q & A
What is the primary topic of the video?
-The video discusses determining the angles of rotation of geometric shapes, specifically triangles and quadrilaterals, under rotation about a point.
How is the angle of rotation determined for triangle ABC to A'B'C'?
-The angle of rotation is determined by observing the movement of point A to A', which shows a counterclockwise rotation of 60 degrees.
What visual clues indicate the direction of rotation?
-The instructor notes that a counterclockwise rotation corresponds to a positive angle, while a clockwise rotation corresponds to a negative angle.
What specific angles are considered in the analysis?
-The angles considered are 30 degrees and 60 degrees for triangle rotation, and right angles for quadrilateral rotation.
Why is 60 degrees chosen as the angle of rotation for triangle ABC?
-60 degrees is chosen because it visually appears to be 2/3 of a right angle, making it more likely than 30 degrees in the context of the triangle's rotation.
What is the angle of rotation for quadrilateral ABCD to A'B'C'D'?
-The angle of rotation for quadrilateral ABCD to A'B'C'D' is -90 degrees, indicating a clockwise rotation.
How does the instructor confirm the angle of rotation for quadrilateral ABCD?
-The instructor analyzes the movement from point D to D' and confirms that the rotation is clockwise, agreeing with the previously determined -90 degrees.
What does the instructor mean by 'ruling out' certain angles?
-'Ruling out' means eliminating angles that do not fit the observed rotation direction or visual evidence, thereby narrowing down the possible angles.
What general approach does the instructor suggest for determining rotation angles?
-The instructor suggests examining the original point and its image after rotation, assessing the visual angle formed, and determining the direction of rotation.
Can this method of determining angles be applied to other geometric shapes?
-Yes, the method can be applied to other geometric shapes by following the same principles of analyzing points and their images under rotation.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Transformasi Geometri [Part 3] - Rotasi (Perputaran)

ROTASI (PERPUTARAN) || TRANSFORMASI GEOMETRI
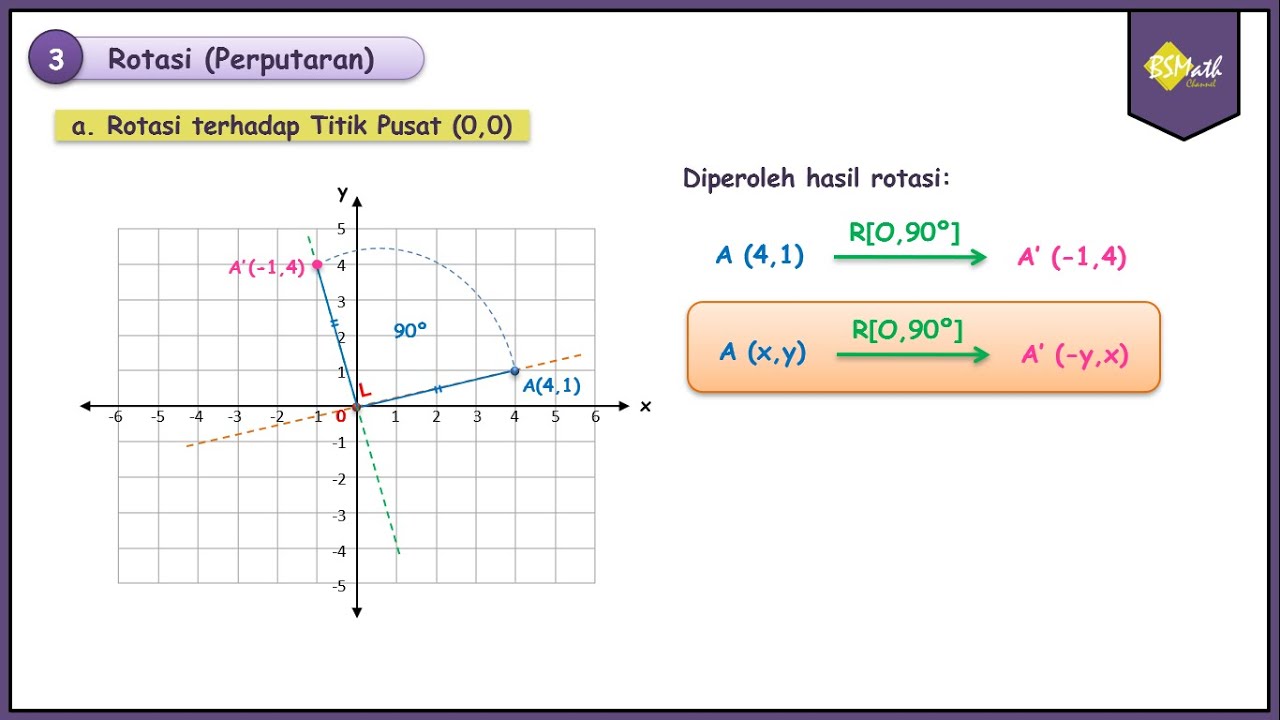
Rotasi Terhadap Titik Pusat O(0,0) - Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka

Math Antics - Angles & Degrees

Kekongruenan Hal 177-180 Bab 3 TRANSFORMASI Kelas 9 SMP Kurikulum Merdeka

Matematika Kelas 9 Bab 3 Transformasi Geometri - A. Translasi hal. 136 - 143 Kurikulum Merdeka
5.0 / 5 (0 votes)
