Lec 38 - Graphs of Polynomials: Multiplicities
Summary
TLDRThis educational video delves into the intricacies of polynomial functions, focusing on identifying their properties, roots, and behaviors through graphical analysis. Viewers learn to discern whether a function is polynomial, find x-intercepts, and understand the impact of root multiplicities on graph shape. The video highlights critical distinctions between odd and even degree polynomials, explaining how these affect the graph's interaction with the x-axis—whether it crosses or bounces off. By mastering these concepts, learners gain a foundational skill set for further exploration in polynomial mathematics.
Takeaways
- 😀 Mastering skills to identify polynomial functions and their roots is essential for understanding polynomial behavior.
- 🔍 Knowledge of x-intercepts and y-intercepts helps visualize the overall shape of polynomial graphs.
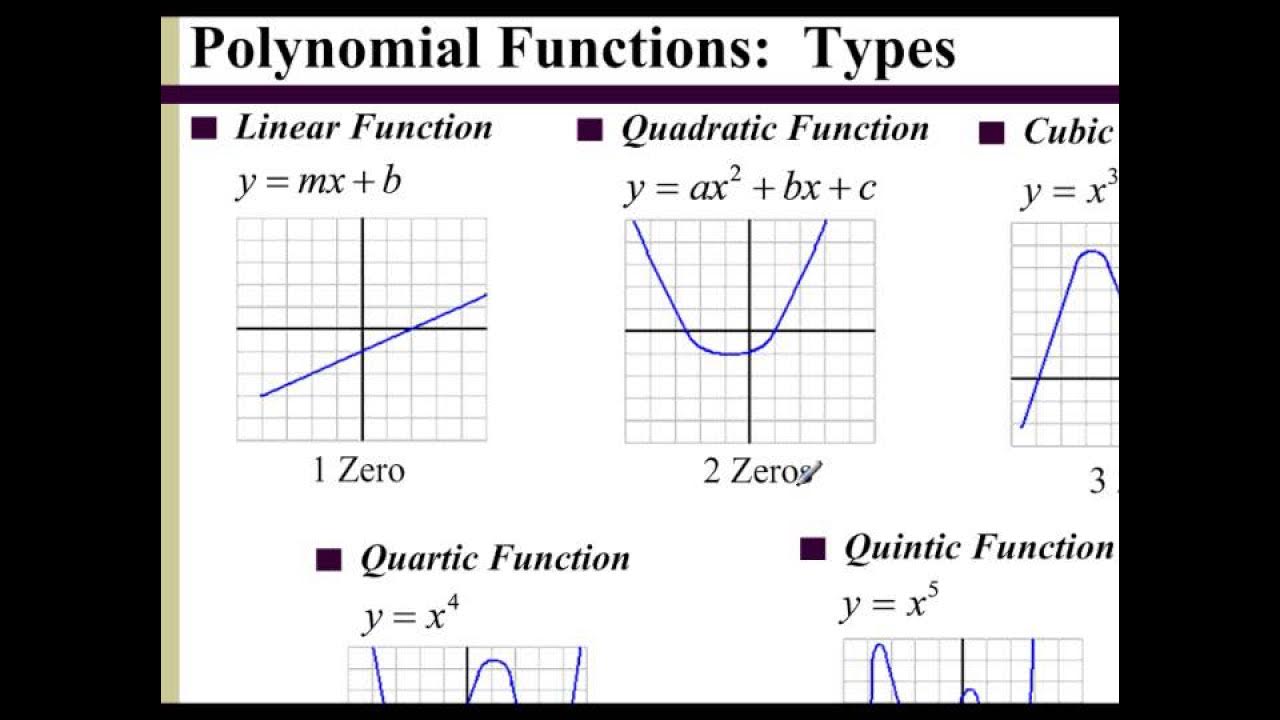
- 📊 The graph of a polynomial function is smooth and can have specific turning points depending on its degree.
- ✏️ Finding x-intercepts can be done through plotting function values at key points when the polynomial is not in factored form.
- 📈 The multiplicity of a root determines how the graph behaves at the x-axis: even multiplicities cause the graph to bounce off, while odd multiplicities allow it to cross.
- 🔗 Polynomial long division can be used to find additional roots once some roots are known.
- 🧩 Understanding the behavior of polynomial graphs around x-intercepts requires knowledge of their multiplicities and degrees.
- 🎨 Odd degree polynomials cross the x-axis, while even degree polynomials touch and bounce off the x-axis.
- ⚖️ The steeper the polynomial's degree, the more pronounced the curve's behavior near its roots.
- 📚 Graphing tools can enhance understanding of polynomial functions by visually representing their characteristics and behaviors.
Q & A
What are the two skills that have been mastered regarding polynomial functions?
-The two skills mastered are identifying whether a given function is a polynomial function and using algebraic expressions to find the roots or zeros of the polynomial.
How can the x-intercepts of a polynomial function be identified?
-X-intercepts can be identified by plotting values of the polynomial function at standard points and observing where the function equals zero.
What is the importance of understanding the multiplicity of a root?
-Understanding the multiplicity of a root helps in determining how the graph behaves at that root, specifically whether it crosses the x-axis or bounces off it.
What is the difference in graph behavior at x-intercepts for even and odd multiplicities?
-Graphs with even multiplicities touch and bounce off the x-axis at the intercept, while graphs with odd multiplicities cross the x-axis.
What is the significance of identifying the roots of a polynomial?
-Identifying the roots allows for constructing the polynomial in factored form, which aids in understanding its graph and behavior.
How does the degree of a polynomial influence its graph?
-The degree of a polynomial affects the number of times it can turn (maximum of degree - 1) and influences whether the graph will cross or bounce at x-intercepts.
What methods can be used to find the roots of a cubic polynomial if it is not in factored form?
-One method is to use polynomial long division after identifying some roots through plotting points and constructing a table of values.
What happens to the graph of a polynomial with higher even degrees near its x-intercepts?
-As the degree increases, the graph appears flatter and broader near the x-intercepts, meaning it will still touch the x-axis but will do so more gently.
Why is it important to use both analytical and graphical tools in understanding polynomial functions?
-Using both tools provides a comprehensive understanding of polynomial behavior, enabling accurate graphing and identification of key features like intercepts and turning points.
Can a cubic polynomial have more than three roots?
-No, a cubic polynomial can have at most three roots, as dictated by its degree.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Graphs of Polynomials: Identification and Characterization

Grade 10 - Illustrating and graphing polynomial functions | SirABC
Lesson 6.3 - Identifying a Polynomial Function from the Graph

Lec 52 - Logarithmic Functions

CBSE Class 11 Maths Project-Relations & Functions

Polinomial (Bagian 5) - Cara Menentukan Akar-akar Persamaan Polinomial
5.0 / 5 (0 votes)
