ASÍNTOTAS VERTICALES y HORIZONTALES 📉 (OBLIGADO VERLO)
Summary
TLDREn este video, se explica el proceso para encontrar asíntotas verticales y horizontales de una función racional. Se comienza determinando el dominio de la función mediante la igualación del denominador a cero, lo que revela las asíntotas verticales en x=1 y x=-1. Luego, se estudian los límites laterales para definir el comportamiento en estos puntos. Finalmente, se analiza la presencia de una asíntota horizontal en y=0 al observar el comportamiento de la función cuando x tiende a infinito. Se concluye con un dibujo que representa estas características clave de la función.
Takeaways
- 📐 El dominio de la función es todos los números reales excepto -1 y 1, ya que el denominador se hace cero en esos puntos.
- ⚠️ Hay asíntotas verticales en x = 1 y x = -1 al igualar el denominador a cero.
- 🔢 Para verificar las asíntotas, se evalúan los límites cuando x tiende a 1 y a -1, comprobando que tienden a infinito.
- ↔️ En x = 1, el límite lateral por la izquierda tiende a menos infinito y por la derecha a más infinito.
- 🔄 En x = -1, el límite lateral por la izquierda tiende a menos infinito y por la derecha a más infinito.
- 📊 Los límites laterales ayudan a determinar el comportamiento de la función cerca de las asíntotas.
- ➖ La función tiene una asíntota horizontal en y = 0 porque el límite cuando x tiende a infinito da cero.
- 🧮 La función no tiene asíntotas oblicuas debido a la existencia de la asíntota horizontal.
- ✍️ Se dibujan las asíntotas verticales en x = 1 y x = -1, y la asíntota horizontal en y = 0.
- 🖍️ El gráfico muestra cómo la función se aproxima a menos infinito o más infinito cerca de las asíntotas verticales, sin tocar la asíntota horizontal.
Q & A
¿Qué función se está analizando en el vídeo?
-La función que se analiza es \( f(x) = \frac{14x + 13}{x^2 - 1} \).
¿Cómo se determina el dominio de la función?
-El dominio se determina igualando el denominador a cero, es decir, \( x^2 - 1 = 0 \), lo que da \( x = 1 \) y \( x = -1 \). Por lo tanto, el dominio son todos los reales excepto 1 y -1.
¿Por qué hay asíntotas verticales en \( x = 1 \) y \( x = -1 \)?
-Hay asíntotas verticales en \( x = 1 \) y \( x = -1 \) porque el denominador se iguala a cero en estos valores, lo que produce una tendencia al infinito en la función.
¿Cómo se comprueba la existencia de una asíntota vertical en \( x = 1 \)?
-Se hace el límite cuando \( x \) tiende a 1. Al sustituir en la función, el numerador da 27 y el denominador tiende a 0, lo que da infinito, confirmando la asíntota vertical.
¿Qué sucede cuando \( x \) tiende a 1 por la izquierda y por la derecha?
-Cuando \( x \) tiende a 1 por la izquierda, la función tiende a menos infinito. Cuando \( x \) tiende a 1 por la derecha, la función tiende a más infinito.
¿Cómo se determina el comportamiento en \( x = -1 \) por la izquierda y la derecha?
-Cuando \( x \) tiende a \( -1 \) por la izquierda, la función tiende a menos infinito, y cuando \( x \) tiende a \( -1 \) por la derecha, la función tiende a más infinito.
¿Cómo se identifica si hay una asíntota horizontal?
-Se hace el límite de la función cuando \( x \) tiende a infinito y a menos infinito. Como el grado del denominador es mayor que el del numerador, el límite tiende a 0, indicando una asíntota horizontal en \( y = 0 \).
¿Por qué no hay asíntotas oblicuas en esta función?
-No hay asíntotas oblicuas porque la función tiene una asíntota horizontal en \( y = 0 \), y si existe una asíntota horizontal, no puede haber una oblicua.
¿Qué importancia tiene el análisis de los límites laterales?
-El análisis de los límites laterales es crucial para determinar hacia qué infinito tiende la función cuando se aproxima a los puntos donde hay asíntotas verticales, lo que ayuda a definir el comportamiento gráfico.
¿Qué características clave presenta el gráfico de esta función?
-El gráfico presenta asíntotas verticales en \( x = 1 \) y \( x = -1 \), y una asíntota horizontal en \( y = 0 \). Además, la función tiende a más o menos infinito dependiendo de si se aproxima a las asíntotas verticales por la izquierda o la derecha.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
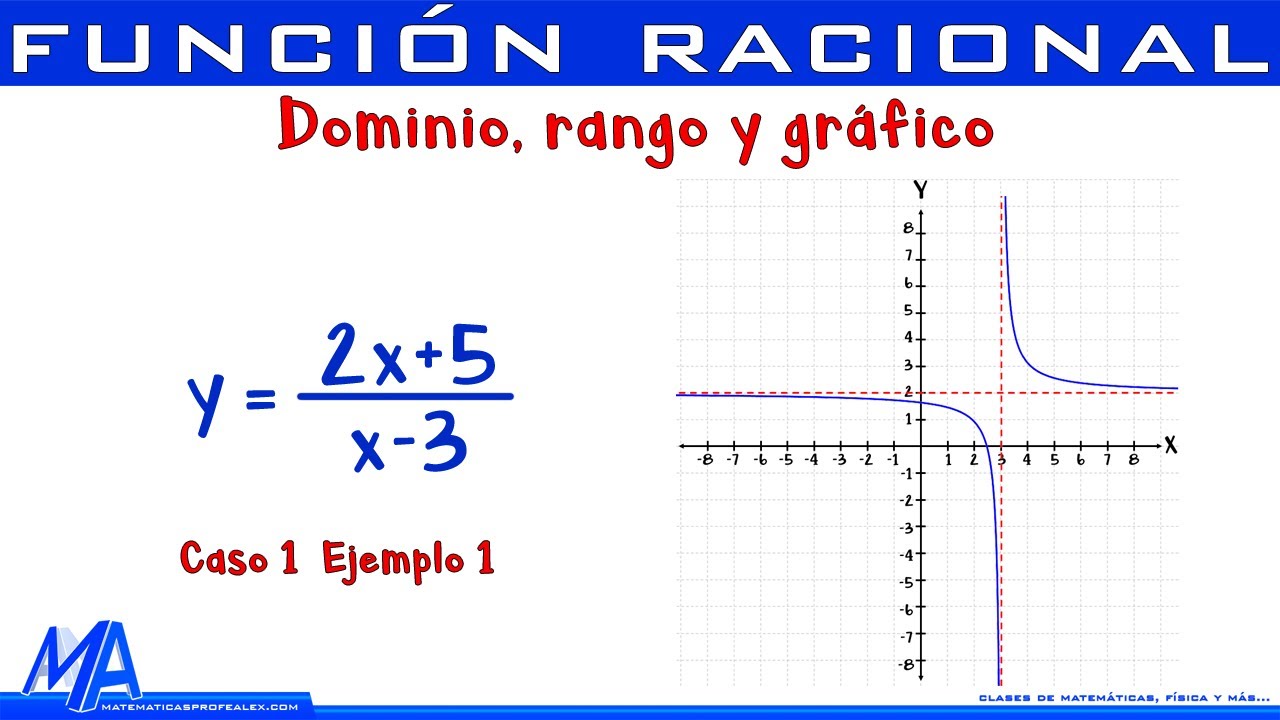
Dominio rango y grafico función Racional | Caso 1 ejemplo 1

Como graficar funciones racionales | Precálculo

Asíntotas verticales, horizontales y oblicuas de una función racional

Función Racional - Ejercicios Nivel 2 - Gráficas

Equilibrio de Cuerpo Rígido, Determinar Reacciones, Estática - Salvador FI

CONSTRUCCIÓN DE CILÍNDROS 2023
5.0 / 5 (0 votes)
