Inverse of One-to-One Function | Grade 11- General Mathematics
Summary
TLDRThis educational video tutorial teaches viewers how to find the inverse of one-to-one functions. It covers three examples: solving for the inverse of a linear function (f(x) = 5x - 8), a rational function (f(x) = (x - 4)/(2x - 7)), and a cubic function (f(x) = 2x^3 - 5). The process involves changing f(x) to y, swapping x and y, solving for y, and simplifying. The video concludes with the inverse functions for each example, encouraging viewers to like and subscribe for more educational content.
Takeaways
- 📕 To find the inverse of a one-to-one function, you first replace f(x) with y.
- 📝 Interchange the variables x and y to reflect the inverse relationship.
- 💵 Solve for y to derive the inverse function.
- 💲 For a linear function like f(x) = 5x - 8, isolate y by transposing terms and dividing by the coefficient.
- 💳 The inverse of f(x) = 5x - 8 is y = (x + 8)/5.
- 📘 For rational expressions, cross-multiply to eliminate the fraction.
- 💴 Group terms with y on one side and terms without y on the other side to isolate y.
- 💹 The inverse of f(x) = (x - 4)/(2x - 7) is y = (7x - 4)/(2x - 1).
- 📗 For functions involving exponents, such as f(x) = 2x^3 - 5, solve for y by transposing and dividing to isolate the cube root.
- 💱 The inverse of f(x) = 2x^3 - 5 is y = √x + 5/2∛.
- 📝 The video provides a step-by-step guide on how to find the inverse of different types of functions, including linear, rational, and cubic functions.
Q & A
What is the first step in finding the inverse of a one-to-one function?
-The first step is to change f(x) to y, so that y equals the function expression.
How do you interchange variables to find the inverse function?
-You interchange x and y variables in the equation to express x in terms of y.
What is the inverse function of f(x) = 5x - 8?
-The inverse function of f(x) = 5x - 8 is x + 8/5.
How do you solve for y in the equation x = 5y - 8 after interchanging variables?
-You transpose -8 to the left side to get +8 and then divide both sides by 5 to isolate y.
What is the process for solving the inverse of a rational function like f(x) = (x - 4)/(2x - 7)?
-You interchange x and y, cross multiply to eliminate the fraction, and then group terms with y on one side and terms without y on the other side.
How do you handle the rational expression after interchanging x and y in f(x) = (x - 4)/(2x - 7)?
-You cross multiply to get rid of the fraction, then rearrange terms to isolate y.
What is the inverse function of f(x) = (x - 4)/(2x - 7)?
-The inverse function of f(x) = (x - 4)/(2x - 7) is 7x - 4/(2x - 1).
How do you solve for y in the equation x = y^3 - 5 after interchanging variables?
-You transpose -5 to the other side to get +5, then divide both sides by 2, and finally take the cube root of both sides.
What is the inverse function of f(x) = 2x^3 - 5?
-The inverse function of f(x) = 2x^3 - 5 is the cube root of (x + 5)/2.
Why is it necessary to cube root both sides after isolating y in the equation x = y^3 - 5?
-You cube root both sides to eliminate the power of 3 on the right side and isolate y.
What does it mean when the inverse function is represented with a negative exponent on y?
-A negative exponent on y indicates that the function is the inverse of the original function.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

INVERSE OF ONE-TO-ONE FUNCTIONS || GRADE 11 GENERAL MATHEMATICS Q1

Functions

Lec 52 - Logarithmic Functions
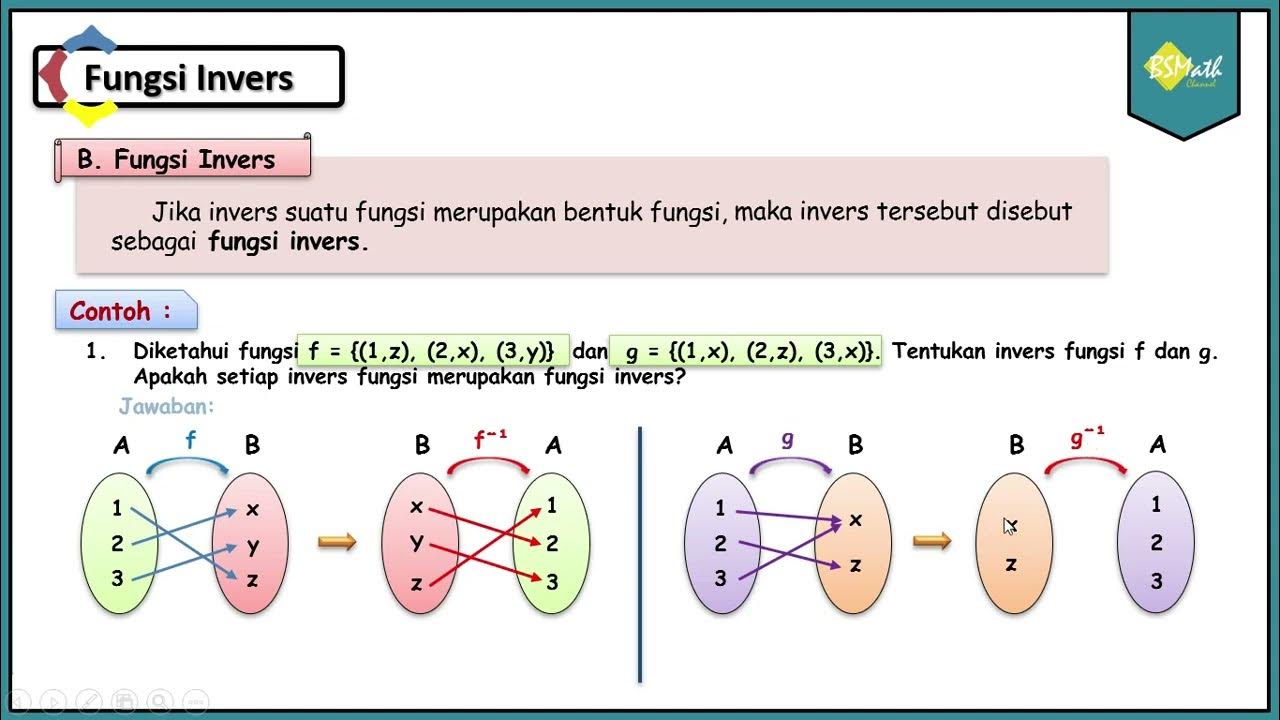
Fungsi Invers - Matematika SMA Kelas XI Kurikulum Merdeka

REPRESENTATIONS OF AN INVERSE FUNCTIONS | General Mathematics | Quarter 1 - Module 13

Komposisi Fungsi Part 3 - Fungsi invers dan Sifat-sifatnya [ Matematika Wajib Kelas X ]
5.0 / 5 (0 votes)
