Solución de límites por factorización | Ejemplo 10
Summary
TLDREn este video se explica cómo resolver límites utilizando la factorización de trinomios de la forma \(x^2 + bx + c\). El instructor guía a los espectadores a través de un ejercicio paso a paso, mostrando dos métodos de factorización para diferentes tipos de trinomios. Además, se aborda la indeterminación y cómo eliminarla al factorizar, todo con un enfoque práctico y directo. Al final, se deja un ejercicio para que los espectadores practiquen, y se invita a revisar videos anteriores sobre límites y factorización para quienes necesiten más apoyo.
Takeaways
- 📘 Este video forma parte de un curso de límites y enseña cómo resolver límites mediante factorización.
- 🔢 Se aborda la factorización de trinomios de la forma \(x^2 + bx + c\) y \(x^2 + bx - c\), donde la diferencia radica en la presencia de un signo más o menos ante el término medio.
- 📐 Se explica que si el trinomio tiene \(x^2\) sin coeficiente, se entiende que es \(x^2\).
- ✅ Se recomienda verificar si la ecuación se puede resolver simplemente reemplazando el valor antes de intentar factorizar.
- 🔄 Se practica la factorización de trinomios ordenando primero los términos y luego buscando dos números que cumplan con ciertas condiciones de multiplicación y suma o resta.
- 📝 Se menciona la importancia de recordar la indeterminación en límites, como \(x^2 - 5\), y cómo buscar un paréntesis que lo resuelva.
- 📖 Se sugiere que si hay dudas en factorización, se revisen los videos anteriores sobre límites y factorización.
- 👉 Se enfatiza la necesidad de factorizar trinomios de forma separada para evitar confusiones.
- 🔢 Se detalla el proceso de factorización paso a paso, incluyendo la multiplicación de coeficientes y la búsqueda de números que cumplan con condiciones específicas.
- 🔄 Se muestra cómo simplificar la factorización al final, extrayendo factores comunes y resolviendo la indeterminación.
- 📑 Se invita a los estudiantes a practicar con ejercicios similares y se ofrecen recursos adicionales para aprender más sobre límites.
Q & A
¿Qué métodos de factorización se discuten en el curso de límites y factorización?
-Se discuten dos métodos de factorización: el trinomio de la forma x^2 + bx + c y el trinomio de la forma x^2 + bx - c.
¿Cuál es la diferencia clave entre los trinomios x^2 + bx + c y x^2 + bx - c?
-La diferencia clave es el signo que acompaña al término medio: el primero tiene una suma (+), mientras que el segundo tiene una resta (-).
¿Cómo se determina si un trinomio puede ser factorizado fácilmente?
-Se verifica si el trinomio tiene la forma x^2 + bx + c o x^2 + bx - c, y si el término que acompaña a x^2 no tiene coeficiente, es decir, es implícito un 1.
¿Qué es la indeterminación en el contexto de los límites?
-La indeterminación se refiere a una expresión que parece no tener una solución clara, como 0/0 o infinito/infinito, que se resuelve al factorizar y simplificar.
¿Cómo se factoriza un trinomio de la forma x^2 + bx + c?
-Se buscan dos números que, al multiplicarse, den el término constante (c) y, al sumarse, den el término de la x (b). Estos números se colocan en dos paréntesis, con el signo correcto en cada uno.
¿Cuál es el primer paso al factorizar un trinomio x^2 + bx - c?
-Es el mismo que para x^2 + bx + c: buscar dos números que multiplicados den el término constante y que sumados den el término de la x.
¿Cómo se identifica la indeterminación en una expresión algebraica?
-Se identifica al observar que la expresión se vuelve de la forma 0/0 o infinito/infinito, lo cual indica que es necesario factorizar y simplificar.
¿Qué significa el signo más y el signo menos en la factorización de trinomios?
-El signo más en el primer paréntesis indica que ambos factores en ese paréntesis son positivos o ambos negativos. El signo menos en el segundo paréntesis indica que uno es positivo y el otro negativo.
¿Cómo se determina el número a colocar en el primer paréntesis al factorizar un trinomio?
-Se coloca el número más grande de los dos que multiplicados dan el término constante y que sumados dan el término de la x.
¿Cuál es la importancia de reemplazar la x con el número dado al resolver un límite?
-Es crucial para encontrar el valor del límite específico, ya que después de simplificar y eliminar la indeterminación, permite evaluar el límite cuando x tiende al número dado.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Solución de límites por factorización | Ejemplo 3

Solución de límites por factorización | Ejemplo 4
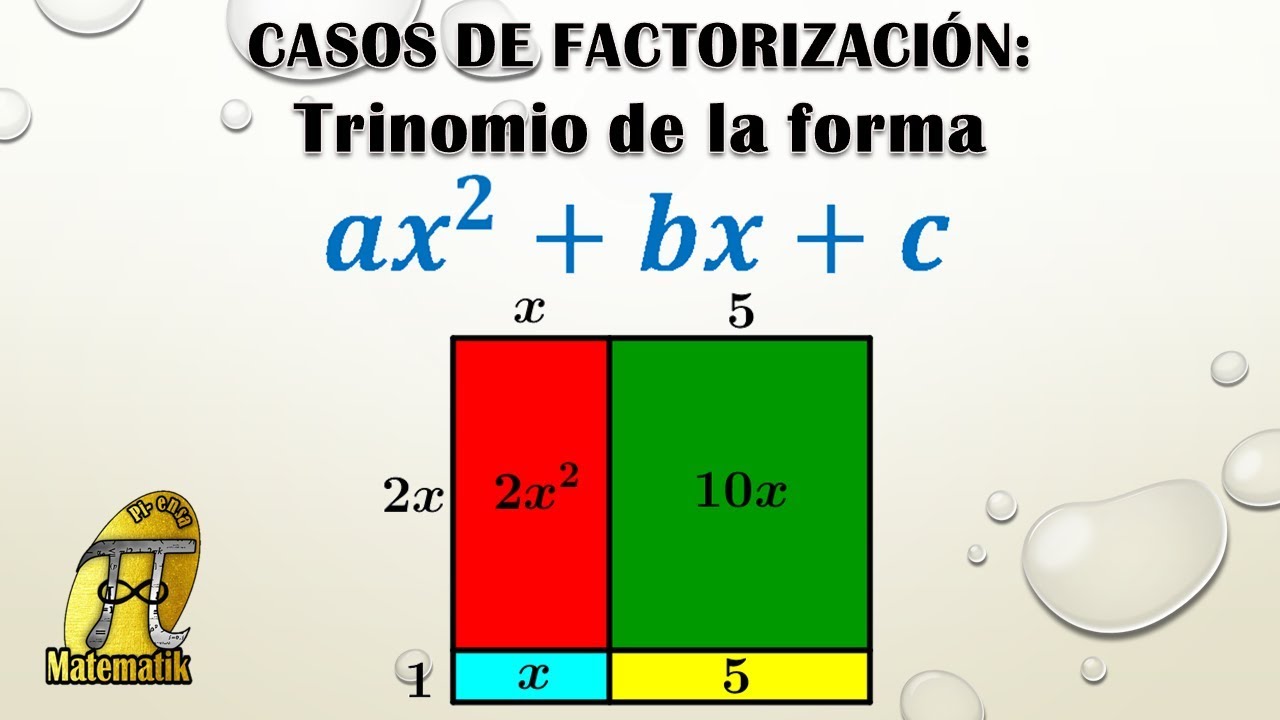
Trinomio de la forma ax^2+bx+c gráficamente | Casos de Factorización

LOS 10 CASOS DE FACTORIZACION En 10 minutos Cursos online

Factorización Trinomio de la forma ax2+bx+c | Paso a paso

Solución de límites por factorización | Ejemplo 6
5.0 / 5 (0 votes)
