Ch 3 Lecture Video, Fall 2024: Measures of Central Tendency
Summary
TLDRThis educational video script delves into the significance of measures of central tendency in statistical analysis, focusing on mode, median, and mean. It explains how these measures help summarize data, revealing patterns and trends. The script clarifies the concept of range, the calculation of mode as the most frequent value, and the median as the middle value in a dataset. It also discusses calculating the mean, emphasizing its importance in various types of data, including interval, ratio, and ordinal. The script provides examples to illustrate these concepts, aiming to enhance understanding of statistical summaries.
Takeaways
- 📊 Measures of central tendency are crucial for summarizing and analyzing data, helping to understand the 'story' the data is telling.
- 🔢 The concept of 'multivariant' data is introduced, referring to datasets with two or more variables, emphasizing the complexity of modern data analysis.
- 📈 Understanding distributions is key, which involves recognizing how data is spread across different variables and values.
- 🎯 Central tendency focuses on identifying the 'middle point' and typical trends within a dataset, aiding in data summarization.
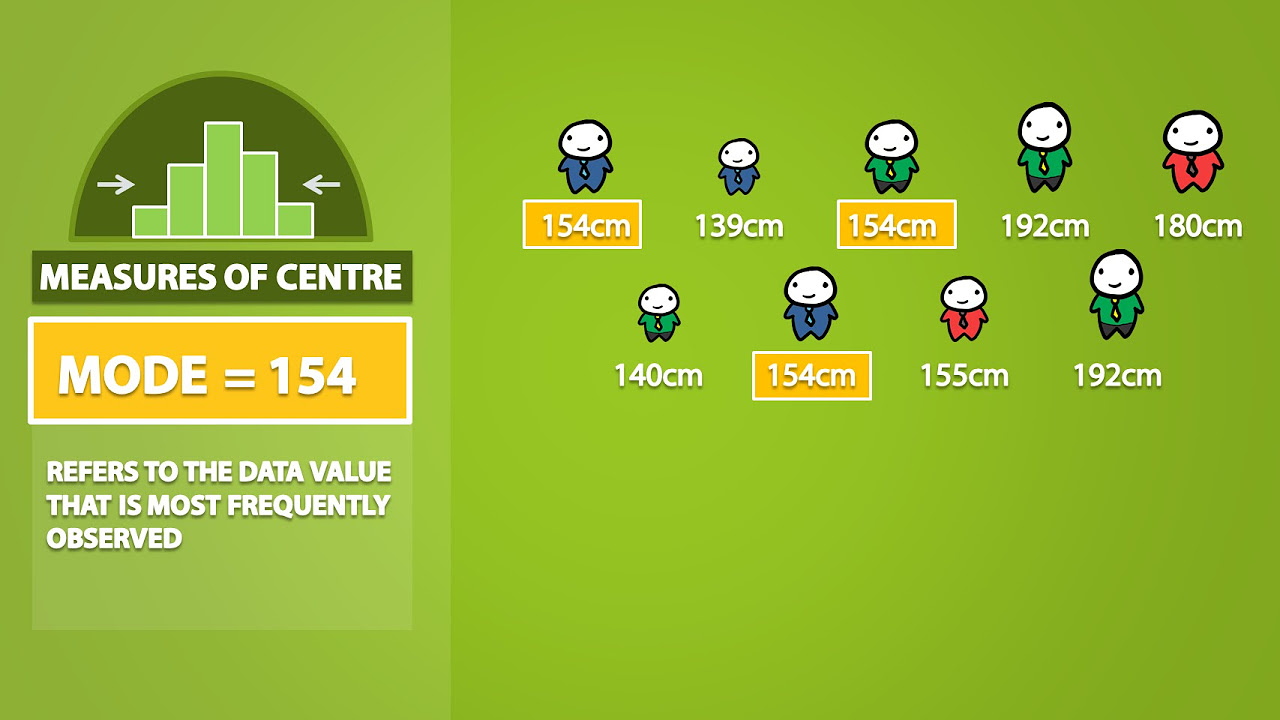
- 🏅 The mode is defined as the most frequently occurring value or category in a dataset, serving as an easy identifier of commonality.
- 🔢 The median is the middle value in a dataset when ordered from least to greatest, dividing the data into halves.
- 📐 The range is calculated as the difference between the highest and lowest values in a dataset, providing a sense of data spread.
- 📊 Percentiles are discussed as a way to understand the relative standing of data points within a dataset, differentiating them from percentages.
- 🧮 The mean, or average, is calculated using the formula \( \bar{Y} = \frac{\sum f \times y}{N} \), where \( f \) is frequency, \( y \) is the value, and \( N \) is the total number of cases.
- ⚖️ Different types of data (nominal, ordinal, interval, ratio) are considered in relation to how they can be analyzed using measures of central tendency, with a clarification that nominal data does not have a mean in the traditional sense.
Q & A
What are the measures of central tendency and why are they important?
-The measures of central tendency include mode, median, and mean. They are important because they help summarize data and provide a better understanding of the typical values or patterns within a dataset, allowing for easier analysis and interpretation.
What is the definition of 'distribution' in the context of statistics?
-In statistics, 'distribution' refers to how values are spread across categories and variables. It looks at the similarities and differences, essentially showing how data points are dispersed.
Can you explain the concept of 'range' in statistics?
-The 'range' in statistics is the difference between the highest and lowest values in a dataset, representing the spread of the data.
What is the mode and how is it determined?
-The mode is the value or category that occurs most frequently in a dataset. It is determined by identifying the data point with the highest frequency.
How is the median calculated for a dataset with an odd number of observations?
-For a dataset with an odd number of observations, the median is calculated by arranging the data in ascending order and selecting the middle value.
What is the formula used to calculate the mean?
-The formula to calculate the mean is the sum of all the values (ΣY) divided by the total number of observations (n), represented as Y Bar = ΣY / n.
How does the calculation of the median differ when the dataset has an even number of observations?
-When the dataset has an even number of observations, the median is the average of the two middle values after the data is arranged in ascending order.
What is the significance of assigning numerical values to non-numerical data?
-Assigning numerical values to non-numerical data allows for statistical analysis and interpretation, such as calculating means or modes, even when the data is ordinal or nominal.
Why can't nominal data be calculated with a mean in the traditional sense?
-Nominal data, which includes categories like gender or eye color, cannot be calculated with a mean in the traditional sense because they do not have a natural order or numerical value that can be averaged.
What is the difference between a percentage and a percentile?
-A percentage represents a proportion of a whole, while a percentile indicates the relative standing of a score within a dataset, showing the percentage of cases that fall below a particular value.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Mean, Median and Mode in Statistics | Statistics Tutorial | MarinStatsLectures
Mode, Median, Mean, Range, and Standard Deviation (1.3)

STATISTIKA: Ukuran gejala pusat dan ukuran letak 1

UKURAN PEMUSATAN DATA BERKELOMPOK | Rataan Median Modus Kuartil Desil Persentil

Statistics: The average | Descriptive statistics | Probability and Statistics | Khan Academy

Statistics - Module 3 - Mean, Median, Mode, Percentiles and Quartiles - Problem 3-1B
5.0 / 5 (0 votes)
