Functions
Summary
TLDRThis educational video script introduces the concept of functions in mathematics, explaining how to identify if a mapping is a function using mapping diagrams and the vertical line test. It covers one-to-one and many-to-one functions, function notation, and how to find the range and domain of a function. The script also discusses excluding values from the domain, composite functions, and finding inverse functions. It provides examples and step-by-step instructions for understanding and applying these mathematical concepts.
Takeaways
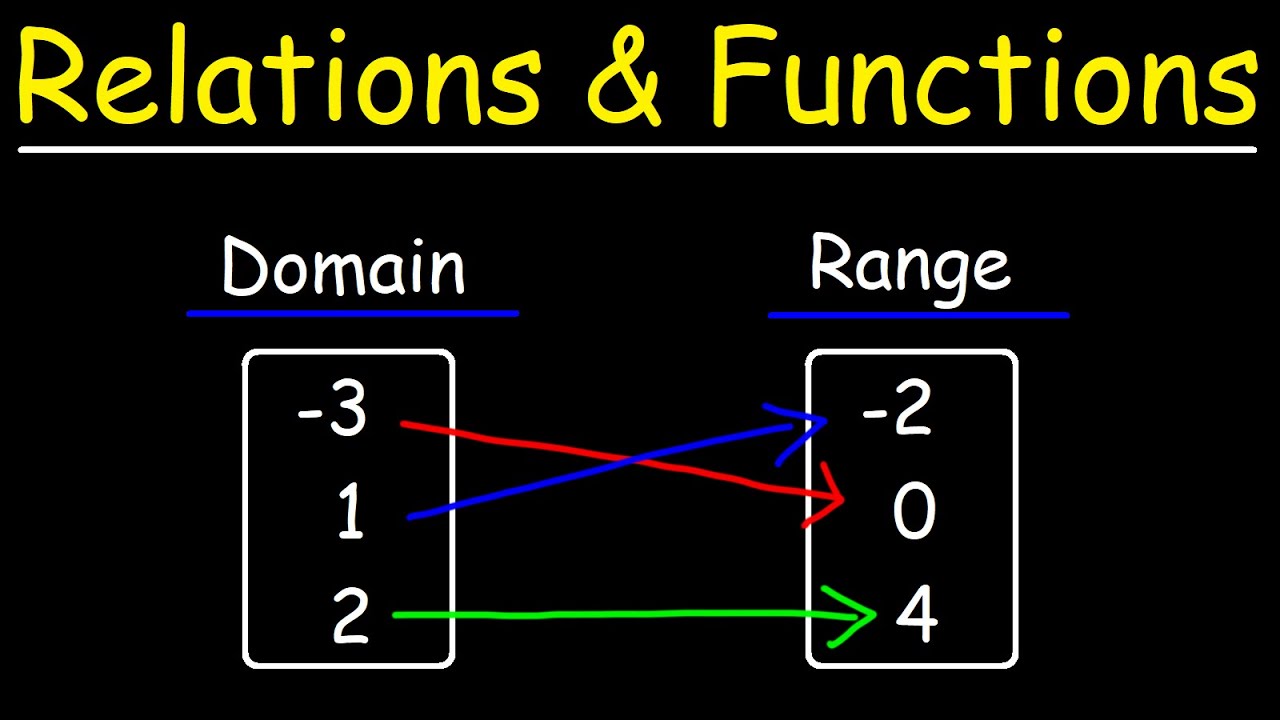
- 🔍 To determine if a mapping is a function, ensure each element in the domain maps to exactly one element in the range.
- 📊 Mapping diagrams and the vertical line test are useful tools to visualize whether a relationship is a function.
- 📐 A one-to-one function is where each element in the domain maps to a unique element in the range, while a many-to-one function has multiple elements in the domain mapping to the same element in the range.
- ❌ Diagrams where elements in the domain map to more than one element in the range, or vice versa, do not represent functions.
- 📝 Function notation, like \( f(x) \), is used to represent the rule by which an input is transformed into an output.
- 🔢 The domain of a function includes all possible input values, while the range consists of all possible output values.
- ⛔ Certain values, like zero in division or negative numbers in square roots, may need to be excluded from the domain as they lead to undefined operations.
- 🔄 Composite functions are created when one function's output becomes the input for another function, with the order affecting the final result.
- 🔄 The notation \( g(f(x)) \) indicates that function \( f \) is applied first, followed by function \( g \).
- 🔙 Inverse functions reverse the action of the original function; if \( f \) adds one, \( f^{-1} \) subtracts one.
- 📉 To find the inverse of a function, rewrite the function as \( y = \), swap \( x \) and \( y \), solve for \( y \), and use the notation \( f^{-1}(x) \).
Q & A
What is a function in mathematical terms?
-A function is a mathematical relationship where each element of one set, called the domain, is associated with exactly one element of another set, called the range.
How can you determine if a mapping is a function using a mapping diagram?
-A mapping is a function if each member of the first set (domain) is connected by exactly one arrow to an element of the second set (range), with no element in the second set being connected to more than one arrow.
What is the difference between a one-to-one function and a many-to-one function?
-A one-to-one function is where each element in the domain maps to a unique element in the range, and each element in the range is mapped to by exactly one element from the domain. A many-to-one function allows multiple elements in the domain to map to the same element in the range.
How do you use the vertical line test to determine if a graph represents a function?
-The vertical line test checks if any vertical line drawn on the graph intersects more than once with the graph. If it intersects only at one point for every vertical line, then the graph represents a function.
What is function notation and how is it used?
-Function notation is a way to represent a function using a symbol, often a letter like 'f'. For example, if 'f(x)' represents a function, then 'f(5) = 10' means that when the input '5' is put into the function 'f', the output is '10'.
Can you explain the concept of domain and range in the context of functions?
-The domain of a function is the set of all possible input values (x-values), while the range is the set of all possible output values (y-values). The domain is what you put into the function, and the range is what you get out of it.
Why are some values excluded from the domain of a function?
-Values are excluded from the domain of a function if they lead to impossible operations, such as division by zero or taking the square root of a negative number, which are undefined in real number arithmetic.
What is a composite function and how is it formed?
-A composite function is formed when one function is followed by another. For example, if you have functions f(x) and g(x), then the composite function g(f(x)) means you first apply f to x, then apply g to the result of f(x).
How do you find the composite function (g ∘ f)(x) given functions f(x) and g(x)?
-To find the composite function (g ∘ f)(x), you first evaluate f(x) to get an output, then use that output as the input for g(x). The result is the value of (g ∘ f)(x).
What is an inverse function and how can you determine if a function has an inverse?
-An inverse function is a function that reverses the effect of the original function. If applying the original function and then its inverse to a number yields the original number, and vice versa, then the function has an inverse. The notation for the inverse of a function f is f^(-1)(x).
How do you find the inverse of a given function algebraically?
-To find the inverse of a function algebraically, you first write the function as y = f(x), then swap x and y to get x = f(y), and finally solve for y to express it in terms of x. This new expression is the inverse function, denoted as f^(-1)(x).
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

THE LANGUAGE OF RELATIONS AND FUNCTIONS || MATHEMATICS IN THE MODERN WORLD

Relations & Functions

FUNCTIONS | SHS GRADE 11 GENERAL MATHEMATICS QUARTER 1 MODULE 1 LESSON 1

REPRESENTATION OF FUNCTIONS ┃Grade 11 General Mathematics
Relations and Functions | Algebra

Introduction to Functions (2 of 2: Examples & Counter-Examples)
5.0 / 5 (0 votes)
