Vectors | Chapter 1, Essence of linear algebra
Summary
TLDRThe video script introduces vectors as the foundational concept in linear algebra, exploring their interpretations from physics, computer science, and mathematics perspectives. It emphasizes the geometric view of vectors as arrows in a coordinate system, rooted at the origin, and their numerical representation as ordered lists or tuples of numbers. The script explains vector addition, a key operation in linear algebra, through the tip-to-tail method and its numerical equivalent, as well as scalar multiplication, which involves stretching or compressing vectors. The summary highlights the importance of understanding these operations for applications in data analysis, physics, and computer graphics, and sets the stage for further exploration of vector concepts like span, bases, and linear dependence.
Takeaways
- 📐 **Vectors Defined**: The script introduces vectors as fundamental to linear algebra, with three perspectives: physics, computer science, and mathematics.
- 🏋️♂️ **Physics Perspective**: In physics, vectors are arrows in space, defined by their magnitude and direction, with position flexibility.
- 💻 **Computer Science Perspective**: From a computer science viewpoint, vectors are ordered lists of numbers, where the order is significant.
- 🔢 **Mathematician's Perspective**: Mathematicians generalize vectors as entities that support vector addition and scalar multiplication, with an abstract approach.
- 📊 **Vector Addition**: Vectors are added by aligning their tails and drawing a new vector from the first tail to the second tip, representing the combined movement.
- 🔄 **Scalar Multiplication**: Multiplying a vector by a scalar (number) stretches or compresses it, with negative scalars reversing direction.
- 📈 **Geometric Interpretation**: The script emphasizes visualizing vectors as arrows in a coordinate system, rooted at the origin for clarity.
- 📝 **Coordinate System**: Coordinates are pairs or triplets of numbers that provide instructions for moving from the origin to the vector's tip in 2D or 3D space.
- 🔗 **Connection Between Views**: Linear algebra's power lies in the ability to switch between the geometric and numerical representations of vectors.
- 🌐 **Applications**: The script highlights linear algebra's utility in data analysis, physics, and computer graphics for pattern recognition and spatial description.
Q & A
What are the three perspectives on vectors mentioned in the script?
-The script mentions three perspectives on vectors: the physics student perspective, the computer science student perspective, and the mathematician's perspective.
How does a physics student typically view vectors?
-From a physics student's perspective, vectors are arrows pointing in space, defined by their length and direction, and can be moved around without changing their identity.
What is the computer science perspective on vectors?
-In computer science, vectors are viewed as ordered lists of numbers, where the order of the numbers is significant.
How does a mathematician generalize the concept of vectors?
-Mathematicians generalize vectors as anything that allows for the operations of vector addition and multiplication by a number, which are abstracted away from their specific representations.
Why are vector addition and multiplication by numbers important in linear algebra?
-Vector addition and multiplication by numbers are fundamental operations in linear algebra because they form the basis for understanding more complex linear algebra concepts.
How is a vector's position in a coordinate system described?
-A vector's position in a coordinate system is described by a pair of numbers in two dimensions or a triplet in three dimensions, which give instructions on how to move from the origin to the vector's tip.
What is the geometric interpretation of vector addition?
-The geometric interpretation of vector addition involves placing the tail of the second vector at the tip of the first and then drawing a new vector from the tail of the first to the tip of the second, representing their sum.
What is the numerical representation of vector addition?
-In numerical terms, vector addition involves matching corresponding components of the vectors and adding them together.
What does it mean to multiply a vector by a number?
-Multiplying a vector by a number, or scalar multiplication, involves stretching or compressing the vector by that factor, or reversing its direction if the number is negative.
Why is the ability to switch between different perspectives of vectors important?
-The ability to switch between different perspectives of vectors is important because it allows for the translation of concepts between the geometric and numerical domains, which is crucial for applications in data analysis, physics, and computer graphics.
What are some upcoming concepts in linear algebra that will be discussed after vectors?
-Some upcoming concepts in linear algebra include span, bases, and linear dependence, which will be explored in subsequent videos.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

LA01_Vectors
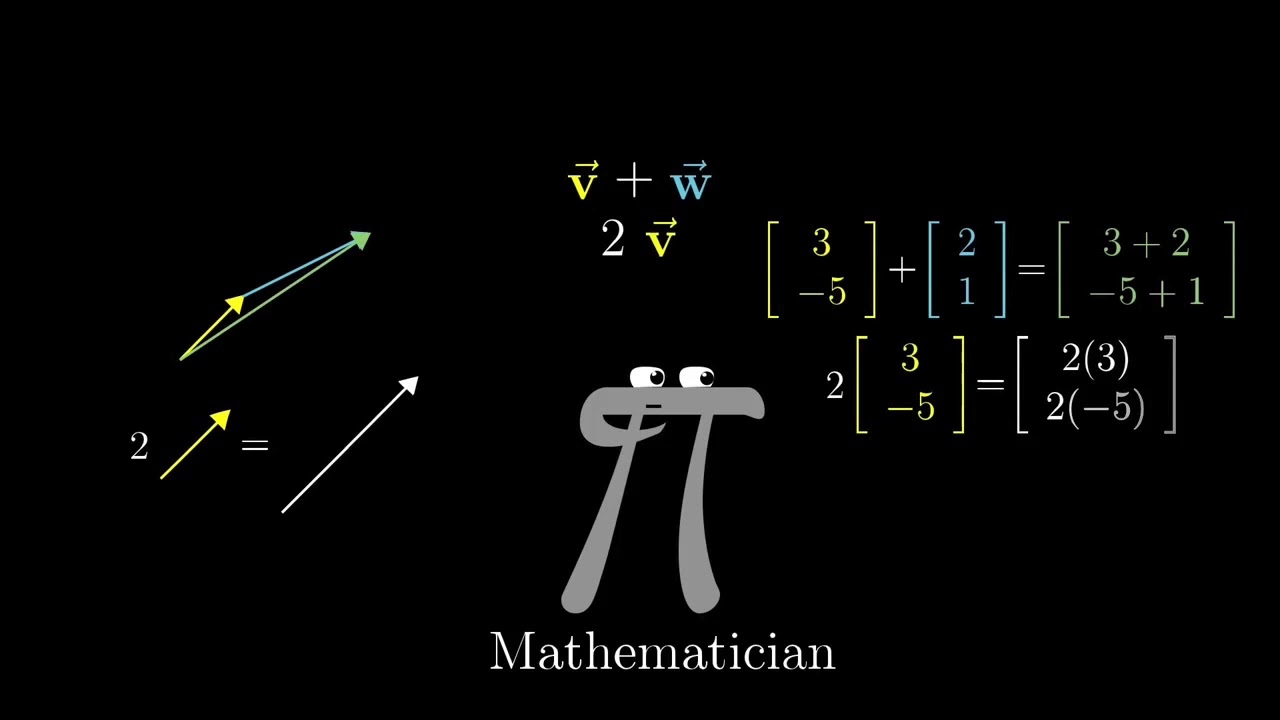
Что такое вектора? | Сущность Линейной Алгебры, глава 1

M4ML - Linear Algebra - 1.1 Introduction: Solving data science challenges with mathematics
Abstract vector spaces | Chapter 16, Essence of linear algebra
Dot products and duality | Chapter 9, Essence of linear algebra

Lecture 36: System of Linear Equations
5.0 / 5 (0 votes)
