Abstract vector spaces | Chapter 16, Essence of linear algebra
Summary
TLDRThis video script delves into the fundamental nature of vectors, exploring whether they are best understood as arrows in a plane or as lists of numbers. It challenges the viewer to consider vectors as spatial entities or manifestations of a deeper concept. The script introduces an analogy between vectors and functions, demonstrating how functions can be treated as vectors by applying principles of linear algebra. Through the lens of linear transformations and the properties of additivity and scaling, the video builds a bridge between abstract mathematical concepts and concrete applications. The script concludes by emphasizing the abstract nature of vectors in modern linear algebra, defined by a set of axioms that allow for a wide range of 'vectorish' objects, including arrows, numbers, functions, and more.
Takeaways
- 🔍 Vectors can be viewed in multiple ways, such as arrows in a plane or pairs of real numbers, and may have deeper spatial properties.
- 📏 Defining vectors as lists of numbers is clear-cut, but they may represent an independent space that coordinates are arbitrarily assigned to.
- 📊 Core linear algebra topics like determinants and eigenvectors are spatial and invariant under changes of coordinate systems.
- 🎯 The essence of vectors might be more about the operations of addition and scaling rather than their representation as numbers or arrows.
- 📚 Functions can also be considered vectors because they support addition and scaling, similar to vectors in linear algebra.
- ✏️ Linear transformations, like the derivative in calculus, can be applied to functions, emphasizing the vector-like qualities of functions.
- 📐 A linear transformation must satisfy additivity and scaling to be considered linear, preserving the operations of vector addition and scalar multiplication.
- 📈 The concept of a matrix can be extended to function spaces, such as polynomials, to describe operations like derivatives.
- 📘 Vector spaces are sets of objects that adhere to the rules of vector addition and scalar multiplication, forming the abstract foundation of linear algebra.
- 📝 Axioms in linear algebra define the properties that vector addition and scalar multiplication must follow, allowing for general application across different types of vector spaces.
- 🎓 The modern theory of linear algebra focuses on abstraction, allowing mathematicians to apply their results to any vector space that satisfies the defined axioms.
Q & A
What is the deceptively simple question the video aims to revisit?
-The video revisits the question of what vectors are, exploring whether they are fundamentally arrows on a flat plane, pairs of real numbers, or manifestations of something deeper.
Why might defining vectors as primarily a list of numbers feel clear-cut and unambiguous?
-Defining vectors as a list of numbers provides a clear and unambiguous way to conceptualize higher-dimensional vectors, making abstract ideas like four-dimensional vectors more concrete and workable.
What is the common sensation among those who work with linear algebra as they become more fluent with changing their basis?
-The common sensation is that they are dealing with a space that exists independently from the coordinates, and that coordinates are somewhat arbitrary, depending on the chosen basis vectors.
Why do determinants and eigenvectors seem indifferent to the choice of coordinate systems?
-Determinants and eigenvectors are core topics in linear algebra that are inherently spatial, and their underlying values do not change with different coordinate systems.
How does the concept of functions relate to the concept of vectors?
-Functions can be seen as another type of vector because they can be added together and scaled by real numbers, similar to how vectors can be combined through addition and scalar multiplication.
What is the formal definition of a linear transformation for functions?
-A linear transformation for functions is defined by two properties: additivity and scaling. Additivity means the transformation of the sum of two functions is the same as the sum of their individual transformations. Scaling means scaling a function and then transforming it yields the same result as transforming the function first and then scaling the result.
Why is the concept of a basis important when dealing with function spaces?
-A basis is important because it provides a coordinate system for the function space, allowing for the representation of functions as vectors with coordinates, which is essential for applying linear algebra concepts to functions.
How is the derivative of a function related to the concept of linear transformations?
-The derivative is an example of a linear transformation for functions. It takes one function and turns it into another while preserving the properties of additivity and scaling.
What is the significance of the matrix representation of the derivative in the context of polynomials?
-The matrix representation of the derivative for polynomials allows for the application of linear algebra techniques to function spaces, specifically polynomial functions, making it possible to visualize and calculate derivatives using matrix-vector multiplication.
What are vector spaces and why are they fundamental in the theory of linear algebra?
-Vector spaces are sets of objects that follow certain rules for vector addition and scalar multiplication, known as axioms. They are fundamental because they provide a general framework for applying linear algebra concepts to various 'vectorish' things, regardless of their specific form or nature.
How does the modern theory of linear algebra approach the concept of vectors?
-The modern theory of linear algebra approaches vectors abstractly, focusing on the axioms that define vector spaces rather than on the specific form vectors take, such as arrows, lists of numbers, or functions.
Why is it beneficial to start learning linear algebra with a concrete, visualizable setting?
-Starting with a concrete, visualizable setting, like 2D space with arrows, helps build intuitions about linear algebra concepts. These intuitions can then be applied more efficiently to more abstract or complex scenarios as one progresses in their understanding of the subject.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Vectors | Chapter 1, Essence of linear algebra

Vektor di Bidang Datar Part 1 (Konsep dan Ruang Lingkup) - Matematika Kelas 12

AQA A’Level Vectors - Part 1, Overview & representation

Plasmid DNA vector in gene cloning | plasmid vector | pbr322 vector | puc 19 vector

(고1 수학 세특 탐구 주제) 복소평면과 복소수 곱을 이용한 점의 회전, 단위근, 수학 보고서 주제, 학생부 종합전형, 수시 준비
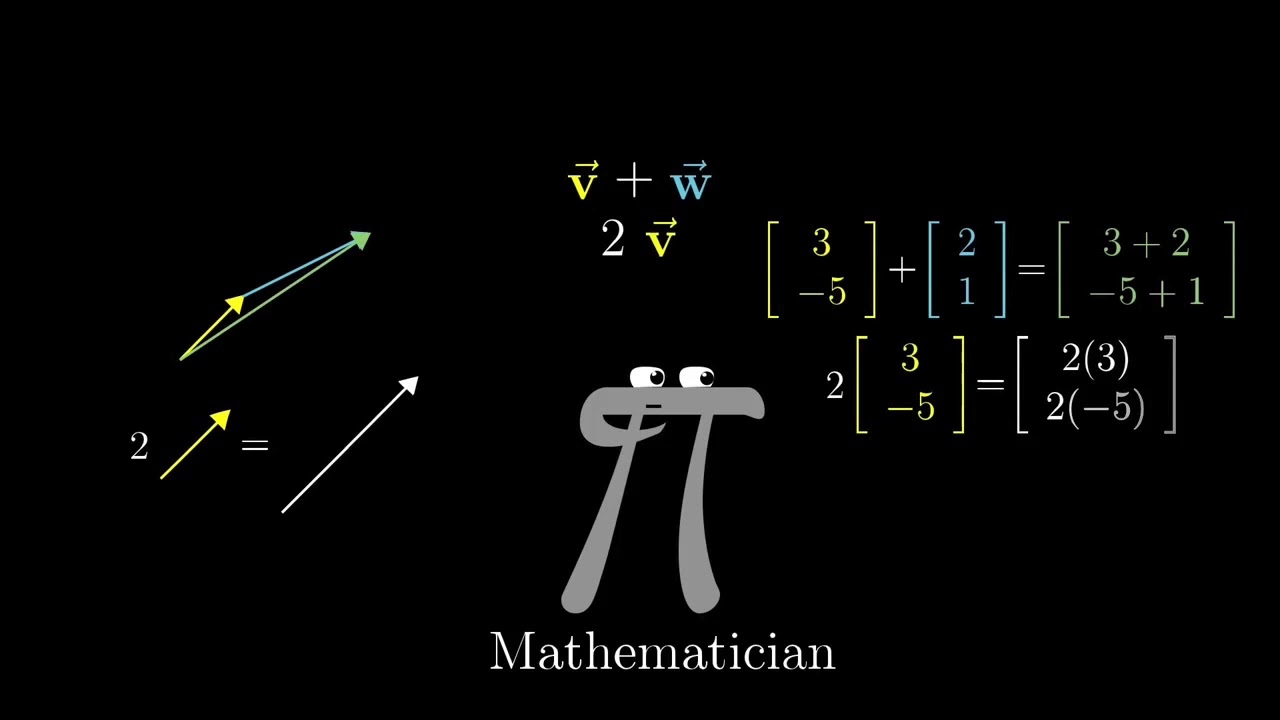
Что такое вектора? | Сущность Линейной Алгебры, глава 1
5.0 / 5 (0 votes)