Distancia entre dos puntos método gráfico
Summary
TLDREn este video tutorial, se enseña cómo calcular la distancia entre dos puntos en un plano utilizando el método gráfico. Se resuelven dos ejercicios prácticos para ilustrar el proceso, que incluye el uso del teorema de Pitágoras para encontrar la hipotenusa de un triángulo rectángulo. Se ofrecen ejemplos visuales y se motiva a los estudiantes a practicar con tres ejercicios adicionales, enfatizando la importancia de comprender las fórmulas detrás de las operaciones y proporcionando una revisión clara y didáctica del tema.
Takeaways
- 📚 Este video forma parte de un curso sobre ecuaciones de rectas y enseña cómo encontrar la distancia entre dos puntos utilizando el método gráfico.
- 📐 Se resuelven dos ejercicios específicos para comprender el concepto de distancia entre puntos en un plano cartesiano.
- 📍 Se utiliza el punto A con coordenadas (1,1) y el punto B con coordenadas (5,4) para ilustrar el primer ejemplo.
- 🔍 Se enseña cómo completar un triángulo rectángulo utilizando la línea de los puntos como hipotenusa y las distancias horizontal y vertical como catetos.
- 📈 Se aplica el teorema de Pitágoras para calcular la distancia, que es la hipotenusa del triángulo rectángulo formado.
- 🔢 Se muestran los cálculos paso a paso, incluyendo la sumación de los cuadrados de los catetos y la extracción de la raíz cuadrada para encontrar la distancia.
- 📉 En el segundo ejemplo, se usan los puntos C (3, -2) y D (-3, 5) para practicar el concepto aprendido.
- 📝 Se sugiere la utilización de hojas cuadriculadas para facilitar la representación gráfica y medición de las distancias en el plano.
- 📐 Se enfatiza la importancia de formar un triángulo rectángulo para aplicar el teorema de Pitágoras y calcular la distancia.
- 📝 Se invita a los espectadores a practicar con tres ejercicios adicionales para reforzar la comprensión del método gráfico.
- 👋 El presentador concluye el video animando a sus espectadores a suscribirse, comentar, compartir y dar like al video para recibir más contenido similar.
Q & A
¿Qué método se utiliza para encontrar la distancia entre dos puntos en el script?
-Se utiliza el método gráfico para encontrar la distancia entre dos puntos.
¿Cuáles son las coordenadas del punto A mencionado en el script?
-Las coordenadas del punto A son (1, 1), donde 1 está en el eje x y 1 en el eje y.
¿Cómo se determina la distancia entre dos puntos utilizando el método gráfico?
-Se forma un triángulo rectángulo con la línea que une los dos puntos como hipotenusa y se utiliza el teorema de Pitágoras para calcular la distancia.
¿Cuántos puntos diferentes se usan para ejemplificar el concepto en el script?
-Se usan cuatro puntos diferentes (A, B, C y D) para ejemplificar el concepto.
¿Qué es lo que se debe recordar sobre el teorema de Pitágoras para aplicarlo correctamente en este caso?
-El teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. En este caso, los catetos son las distancias horizontal y vertical entre los puntos.
¿Cómo se determina si los triángulos formados son semejantes según el script?
-Los triángulos son semejantes si tienen las mismas medidas en sus catetos, lo cual se verifica en el script al comparar las distancias en los triángulos formados por los puntos A y B, y C y D.
¿Cuál es la fórmula que se utiliza para calcular la distancia entre dos puntos (hipotenusa) según el script?
-La fórmula utilizada es la raíz cuadrada de (cateto1 al cuadrado + cateto2 al cuadrado), donde cateto1 y cateto2 son las distancias horizontal y vertical respectivamente.
¿Qué unidades de medida se usan para las coordenadas en el script?
-Las unidades de medida para las coordenadas son 'unidades' o 'cuadritos' en el script, sin especificar una unidad de medida real.
¿Cómo se resuelve el ejercicio de encontrar la distancia entre los puntos C y D según el script?
-Se trazan las coordenadas de los puntos C y D, se forma un triángulo rectángulo con la recta que une los puntos como hipotenusa, y se aplican los catetos medidas para calcular la distancia utilizando el teorema de Pitágoras.
¿Qué herramienta se sugiere para encontrar una raíz cuadrada que no sea exacta en el script?
-Se sugiere usar una calculadora para encontrar una raíz cuadrada que no sea exacta.
¿Qué se ofrece al final del script para los espectadores?
-Se ofrece un desafío de tres ejercicios para practicar el concepto de distancia entre puntos, y se invita a los espectadores a suscribirse, comentar, compartir y dar like al video.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Distancia entre dos puntos, usando Teorema de Pitágoras

Distancia entre dos puntos ejemplo 3 método gráfico

1. Distancia entre dos puntos. Deducción de la fórmula y ejemplos

Suma de Vectores MÉTODO DEL POLÍGONO 📏✏📐 paso a paso

LEVANTAMIENTO DE UN TERRENO POR COORDENADAS
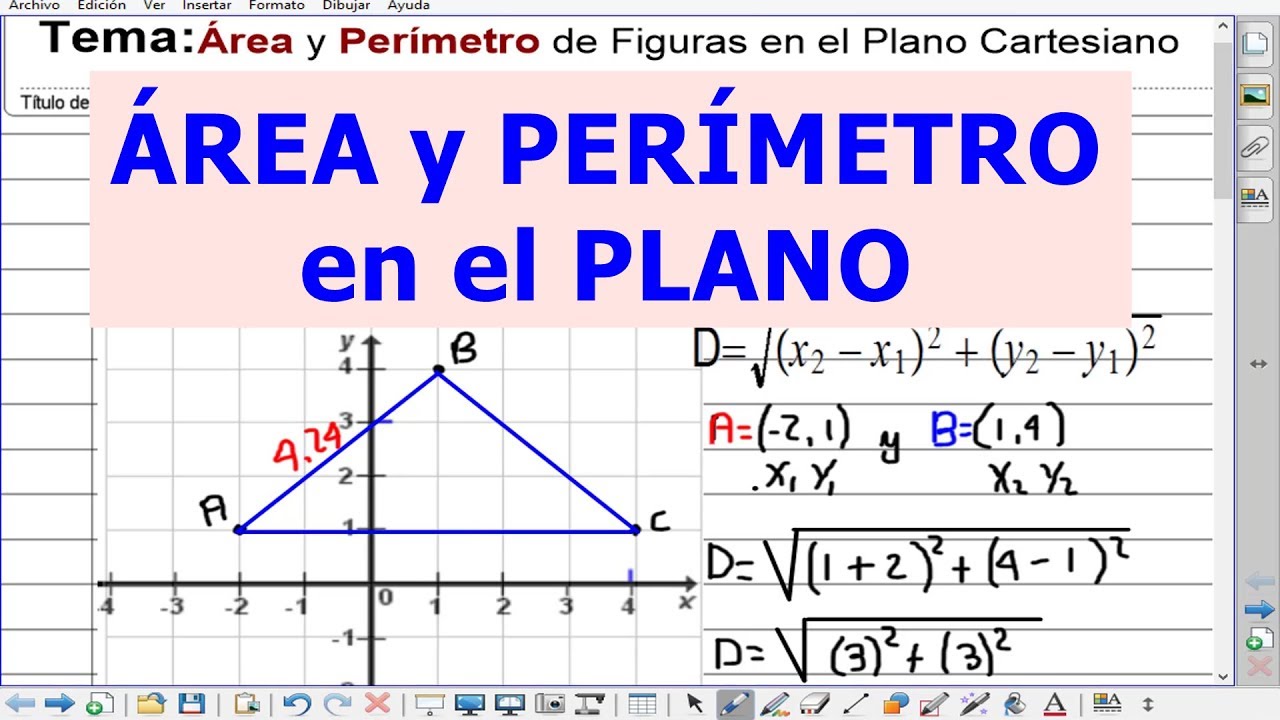
Área y Perímetro de Figuras en el Plano Cartesiano.
5.0 / 5 (0 votes)
