Divergence and Curl of vector field | Irrotational & Solenoidal vector
Summary
TLDRThe video script delves into the concepts of divergence and curl, fundamental to vector calculus, exploring their definitions, applications, and significance in understanding fluid dynamics and electromagnetic fields. It offers a comprehensive look at how these vector operations reveal the behavior of fields, crucial for students and professionals in engineering and physics.
Takeaways
- 📚 Divergence measures the rate at which a vector field is spreading out or converging at a given point.
- 🌀 Curl quantifies the rotation or circulation of a vector field around a point.
- 🧭 Both divergence and curl are scalar and vector operations, respectively, applied to vector fields.
- 📉 Divergence is a scalar that indicates the net flow out of an infinitesimal volume in the field.
- 🔄 Curl is a vector that represents the axis and magnitude of the rotation of the field around a point.
- 🤔 Understanding divergence and curl is crucial for solving problems in fluid dynamics and electromagnetism.
- 🌐 The operation of divergence is denoted as 'div' and curl as 'curl' in mathematical notation.
- 🔍 Divergence can be visualized as the source or sink of a field, indicating creation or annihilation of field lines.
- 🌀 The curl can be visualized by the right-hand rule, which shows the direction of rotation around a point.
- 📐 Both divergence and curl are calculated using partial derivatives in a coordinate system.
- 🔧 They are fundamental in the study of vector calculus and have applications in physics and engineering.
Q & A
What is the divergence of a vector field?
-The divergence of a vector field is a scalar function that measures the magnitude of a source or sink at a given point, or the rate at which the vector field is spreading out or converging at that point.
What is the curl of a vector field?
-The curl of a vector field is a vector function that represents the rotation or circulation of the field around a certain point, indicating the tendency of the field to induce rotation.
How is the divergence related to the density of a fluid?
-In fluid dynamics, the divergence of the velocity vector field is related to the rate of change of fluid density, indicating areas where the fluid is expanding or compressing.
What physical interpretation does the curl have in terms of fluid flow?
-In fluid flow, the curl can be interpreted as twice the local vorticity, which is a measure of the rotation or swirling motion of the fluid.
How can the divergence and curl be used in electromagnetism?
-In electromagnetism, the divergence of the electric field is related to the charge density, while the curl of the magnetic field (in a steady state) is related to the electric field, as described by Maxwell's equations.
What is the mathematical expression for the divergence of a vector field in Cartesian coordinates?
-In Cartesian coordinates, the divergence of a vector field F = (Fx, Fy, Fz) is given by ∇ ⋅ F = ∂Fx/∂x + ∂Fy/∂y + ∂Fz/∂z.
What is the mathematical expression for the curl of a vector field in Cartesian coordinates?
-In Cartesian coordinates, the curl of a vector field F = (Fx, Fy, Fz) is given by ∇ × F = (∂Fz/∂y - ∂Fy/∂z)i + (∂Fx/∂z - ∂Fz/∂x)j + (∂Fy/∂x - ∂Fx/∂y)k.
Can the curl of a vector field be zero everywhere?
-Yes, a vector field can have a curl of zero everywhere, which means it is an irrotational field and has no local rotation or swirling motion.
What does it mean if the divergence of a vector field is zero everywhere?
-If the divergence of a vector field is zero everywhere, it is called a solenoidal field, indicating that there are no sources or sinks in the field, and the field lines do not begin or end anywhere.
How can one visualize the divergence and curl of a vector field?
-Divergence can be visualized as the rate at which field lines are spreading out or converging, while curl can be visualized by the tendency of the field lines to form closed loops, indicating rotation.
Are there any constraints on the relationship between divergence and curl for a vector field?
-In general, there are no direct constraints on the relationship between divergence and curl for a vector field. However, certain physical laws, like the conservation of mass or Gauss's law, may impose specific relationships in certain contexts.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
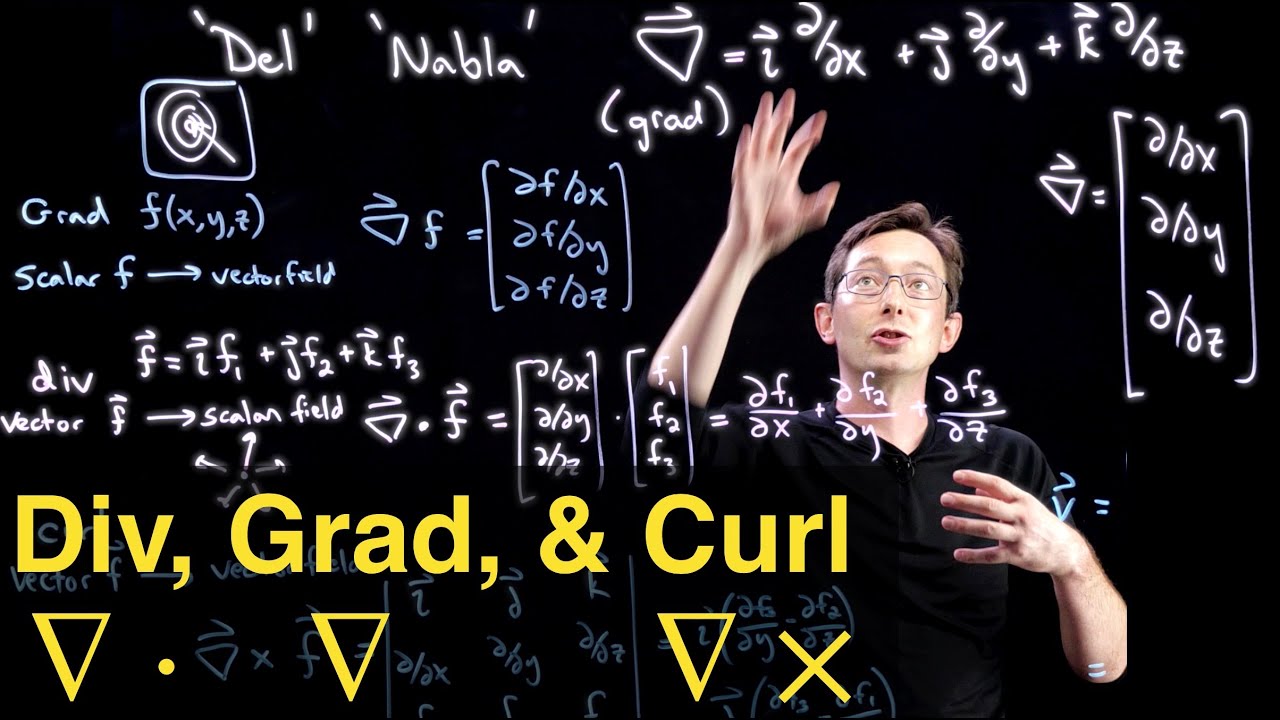
Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]

This Downward Pointing Triangle Means Grad Div and Curl in Vector Calculus (Nabla / Del) by Parth G

The Curl of a Vector Field: Measuring Rotation

Aula 3.5 - Teorema de Helmholtz e Exercícios

Concept of Vector Point Function & Vector Differentiation By GP Sir

M172 - Operator Diferensial Vektor : Del atau Nabla,memahami secara mudah
5.0 / 5 (0 votes)
