ADM1305 - Section 2.4 (Part 3)
Summary
TLDRIn this instructional video, the presenter guides viewers through solving a system of linear equations with three equations and four unknowns using Gaussian elimination. The process involves constructing an augmented matrix, identifying pivots, performing row operations to achieve row-echelon form, and ultimately, reducing the matrix to its simplest form to determine the system has infinitely many solutions. The presenter emphasizes the importance of careful calculations and provides a methodical approach to finding the general solution in canonical form, highlighting the role of free and dependent variables.
Takeaways
- 📚 The video is a tutorial on solving a system of linear equations with three equations and four unknowns using the Gaussian elimination algorithm.
- 🔍 The system is represented by an augmented matrix, which is constructed from the given equations.
- 🎯 The first step in the algorithm is to find a pivot in the first row and first column to simplify the matrix.
- 🛠️ Elimination steps are performed to zero out the entries below the pivot in the first column.
- 🔄 The process involves subtracting multiples of the first row from the other rows to achieve a zero in the first column below the pivot.
- 📉 After the first elimination, the matrix is updated, and the next pivot is identified in the second row and third column.
- ✂️ A simple elimination is done to remove the one below the new pivot in the third row.
- 📊 The matrix is then transformed into its row-echelon form (REF), which allows for the analysis of the system's solutions.
- 🔑 The presence of more variables than the rank of the matrix indicates that the system has infinitely many solutions.
- 🔍 The final step is to convert the REF matrix into its reduced row-echelon form (RREF) to find the general solution.
- 📝 The general solution is expressed in terms of a free variable (X in this case) and the dependent variables (W, Y, Z).
- 📈 The video concludes with the presentation of the general solution in canonical form, showing how to express each variable as a function of the free variable.
Q & A
What is the method used in the video to solve the system of linear equations?
-The method used in the video is Gaussian elimination, specifically aiming to achieve the matrix in row-echelon form and then in reduced row-echelon form.
How many equations and unknowns are in the system presented in the video?
-The system has three equations and four unknowns, represented by the variables W, X, Y, and Z.
What is the augmented matrix mentioned in the video?
-The augmented matrix is a matrix derived from a system of linear equations, where the coefficients of the variables form the left part of the matrix and the constants form the right part, creating a bridge between the coefficients and the constants.
Why is it important to have the correct first pivot when using Gaussian elimination?
-Having the correct first pivot is crucial because it sets the foundation for the subsequent elimination steps. If the first pivot is incorrect, it can lead to errors throughout the entire matrix, ultimately affecting the solution.
What does the video suggest doing with the entries below the first pivot in the first column?
-The video suggests performing eliminations to destroy the entries below the first pivot in the first column, specifically to eliminate the W terms in the second and third equations.
What is the purpose of the elimination steps shown in the video?
-The purpose of the elimination steps is to create zeros below the pivot elements, which helps in simplifying the matrix and moving towards the row-echelon form and eventually the reduced row-echelon form.
What does the video mean by 'rescaling' a row?
-Rescaling a row in the context of the video means multiplying the entire row by a scalar to make the pivot element equal to one, which simplifies the matrix and makes it easier to interpret.
How does the video determine the general solution of the system?
-The video determines the general solution by using the reduced row-echelon form of the matrix, identifying free variables, and expressing the dependent variables in terms of these free variables.
What is the significance of the number of variables being greater than the rank in the system?
-When the number of variables is greater than the rank of the matrix, it indicates that there are more variables than independent equations, which means the system has infinitely many solutions.
How does the video present the final solution of the system?
-The video presents the final solution in canonical form, which involves expressing the dependent variables in terms of the free variables and organizing the solution into a clear and structured format with constants and variable coefficients separated.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
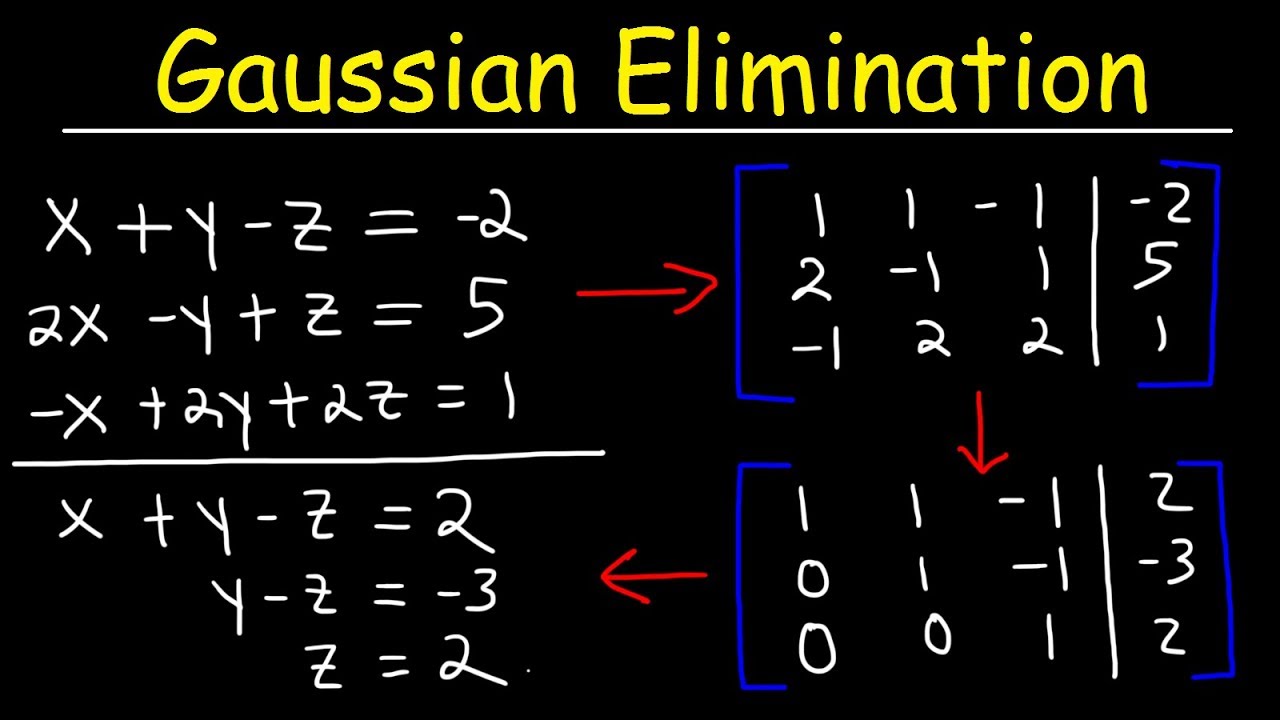
Gaussian Elimination & Row Echelon Form

Sistem Persamaan Linear Tiga Variabel (SPLTV) | Matematika Wajib Kelas X
Gaussian elimination | Lecture 10 | Matrix Algebra for Engineers

Sistem Persamaan Linear Tiga Variabel (SPLTV) membuat model matematika | by Iga Apriliana Mahardika

SPLTV #Part 4 // Metode Gabungan // Sistem Persamaan Linear Tiga Variabel

SPLDV - Metode Eliminasi
5.0 / 5 (0 votes)
