This equation will change how you see the world (the logistic map)
Summary
TLDRThis video explores the surprising connections between diverse phenomena like dripping faucets, rabbit populations, thermal convection, and neuron firing, all governed by a simple logistic equation. It delves into the concept of chaos theory, illustrating how small changes can lead to unpredictable outcomes. The script discusses the logistic map's journey from stable equilibrium to chaotic behavior as growth rates increase, and how this pattern mirrors the Mandelbrot set's fractal structure. The video also highlights the Feigenbaum constant, a universal ratio observed in bifurcation processes, emphasizing the profound impact of a simple equation across various scientific fields.
Takeaways
- 📈 The logistic map is a simple equation that models population growth with environmental constraints, leading to complex behaviors like equilibrium and chaos.
- 🐰 The population of rabbits can be modeled using the logistic map, where the growth rate and initial population size affect long-term behavior.
- 🔢 The logistic map equation can lead to stable equilibrium, periodic oscillations, and chaotic behavior depending on the growth rate parameter.
- 🔁 Period doubling is a phenomenon where a system transitions from a stable state to oscillating between two, then four, and so on, values before becoming chaotic.
- 🌀 The bifurcation diagram, which shows the stable states of a system over a range of parameters, resembles a fractal and is part of the Mandelbrot set.
- 🌐 The Mandelbrot set is a famous fractal based on the iteration of a complex equation, and it includes the bifurcation diagram within its structure.
- 🔬 Scientific experiments have confirmed the logistic map's predictions in various fields, including fluid dynamics, eye response to flickering lights, and heart fibrillation.
- 💧 The dripping faucet is an example of a system that can exhibit period doubling and chaos, challenging the perception of its regularity.
- 🔢 The Feigenbaum constant (approximately 4.669) is a universal constant that describes the rate at which bifurcations occur in systems with single-hump functions.
- 🌐 Universality in chaos theory suggests that similar behaviors and constants appear across different systems and equations, indicating a fundamental aspect of nature.
- 📚 The logistic map and its implications have been influential in scientific research, prompting a call for teaching these concepts to students to foster a deeper understanding of complexity from simplicity.
Q & A
What is the logistic map equation used for modeling population growth?
-The logistic map equation is used for modeling population growth by considering both the growth rate and the carrying capacity of the environment. It is given by the formula x_{n+1} = R * x_n * (1 - x_n), where x_n is the population at time 'n', and 'R' is the growth rate.
Why does the simple exponential growth model fail to accurately represent real-world population growth?
-The simple exponential growth model fails because it suggests that the population would grow indefinitely, which is unrealistic. The logistic map introduces a term to represent environmental constraints, preventing the population from exceeding the carrying capacity.
What is the significance of the value 'R' in the logistic map equation?
-The value 'R' in the logistic map equation represents the growth rate of the population. It is a key parameter that influences the behavior of the population over time, including whether the population stabilizes, oscillates, or enters a chaotic state.
How does the logistic map equation demonstrate a negative feedback loop?
-The logistic map demonstrates a negative feedback loop through the term (1 - x_n). As the population size x_n approaches the carrying capacity, this term approaches zero, thus reducing the growth rate and preventing the population from exceeding the environmental limits.
What is the Feigenbaum constant and what does it represent?
-The Feigenbaum constant, approximately 4.669, represents the universal ratio at which bifurcations occur in systems that exhibit period doubling as they approach a chaotic state. It is a fundamental constant found in many different mathematical and physical systems.
What is a bifurcation diagram and how is it related to the logistic map?
-A bifurcation diagram is a graphical representation of the stable states of a system as a function of a bifurcation parameter. In the context of the logistic map, it shows how the equilibrium population changes with the growth rate 'R', revealing patterns of period doubling and chaos.
How does the logistic map equation relate to the Mandelbrot set?
-The logistic map equation is related to the Mandelbrot set because the bifurcation diagram of the logistic map is part of the Mandelbrot set when viewed in the complex plane. The behavior of the logistic map iterations mirrors the structure of the Mandelbrot set.
What is the connection between the logistic map and thermal convection in a fluid?
-The logistic map's pattern of period doubling and chaos has been experimentally observed in thermal convection in a fluid, such as in the case of a fluid dynamicist's experiment with mercury in a temperature gradient, demonstrating the universality of the logistic map's behavior in different physical systems.
How has the logistic map been applied to understand heart fibrillation in medical research?
-The logistic map has been used to model the progression to heart fibrillation, showing a period doubling route to chaos in the heart's beating pattern. This understanding has been applied to develop smarter ways to deliver electrical shocks to restore normal heart rhythm.
What is the significance of the Feigenbaum constant in understanding universality in chaotic systems?
-The Feigenbaum constant signifies the universality of the period-doubling route to chaos across different systems and equations. Its presence indicates a fundamental process that is independent of the specific form of the equation, suggesting a deeper underlying principle in nature.
How does the logistic map equation apply to the study of dripping faucets and their behavior?
-The logistic map equation can model the behavior of dripping faucets, showing how an initially regular dripping pattern can transition into period doubling and eventually chaotic behavior as the flow rate is adjusted, demonstrating the equation's applicability to seemingly simple real-world phenomena.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
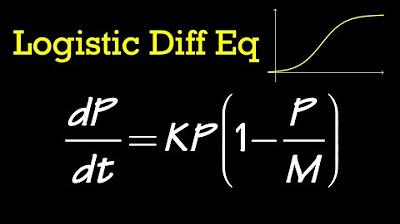
Logistic Differential Equation (general solution)

Water Saving Tips and Tricks - Let's Save the Planet - The Environment for Kids

PDE 2 | Three fundamental examples

CONVECÇÃO TÉRMICA (Física - 2o ANO)

How to Prevent Frozen and Burst Pipes | Ask This Old House

AQA Psychology Biopsychology The Synapse. Video No. 9
5.0 / 5 (0 votes)
