G-5. Breadth-First Search (BFS) | C++ and Java | Traversal Technique in Graphs

Summary

In this video, the instructor explains the breadth-first search (BFS) algorithm, a critical graph traversal technique. BFS is a level-wise approach where nodes are visited in order of increasing distance from a starting node. The tutorial walks through an example graph, discussing key concepts such as node levels and the use of a queue for traversal. The importance of marking nodes as visited to prevent revisiting is emphasized. Additionally, the video covers initial configuration, including the queue data structure and visited array. Finally, the instructor demonstrates BFS coding in C++ and Java, explaining the space and time complexity of the algorithm.

Takeaways

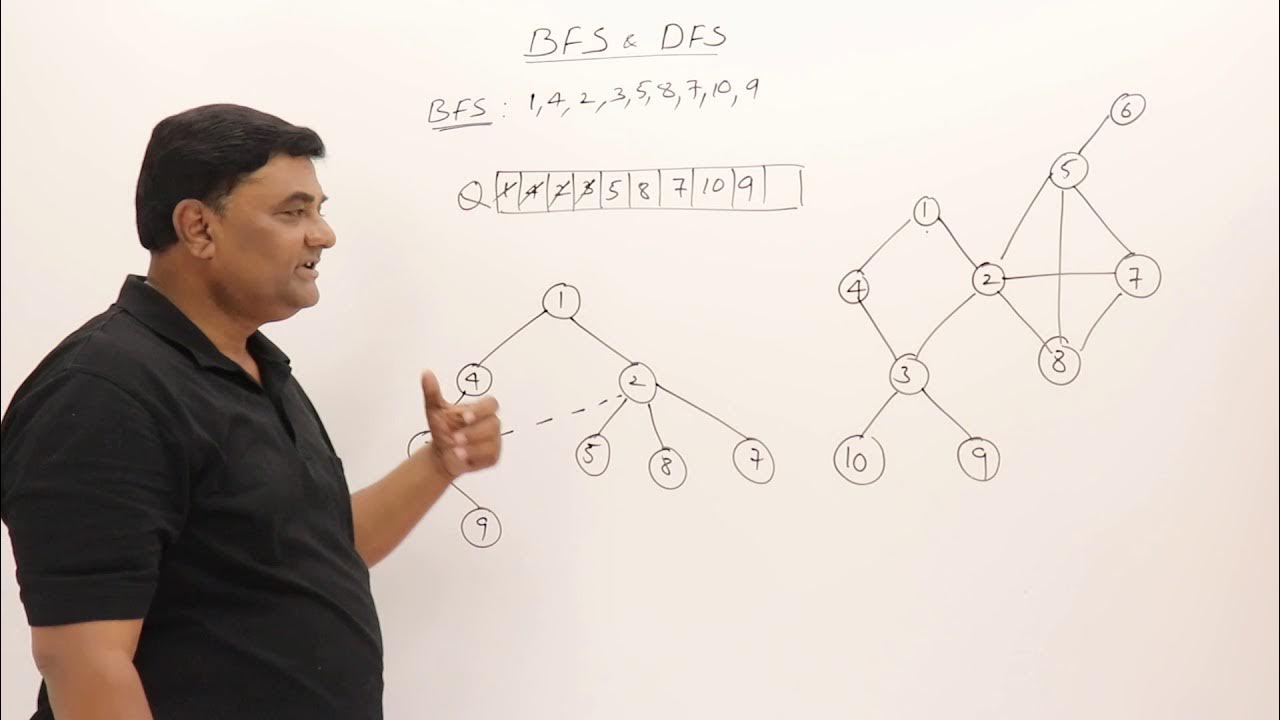
• 📘 Breadth First Search (BFS) is a graph traversal technique that explores nodes level by level, starting from a given node.
• 🔢 BFS can be applied to both 0-based and 1-based indexed graphs, with only minor changes in implementation.
• 📊 The key concept of BFS is 'breadth' — it visits all nodes at the current level before moving to the next level.
• 🧮 The starting node is always considered as level 0, and its directly connected nodes form level 1, and so on.
• 🧱 BFS uses a Queue data structure (FIFO – First In First Out) to manage nodes to be visited next.
• 🚦 A 'visited' array is essential to keep track of nodes that have already been traversed, preventing duplicates.
• 🔗 The adjacency list is used to represent the graph, where each node stores its neighboring nodes.
• ⚙️ The BFS algorithm repeatedly dequeues a node, processes it, and enqueues all its unvisited neighbors while marking them as visited.
• 💻 In C++ or Java implementation, BFS involves initializing a queue, marking the start node as visited, and iterating until the queue becomes empty.
• ⏱️ The time complexity of BFS is O(N + E), where N is the number of nodes and E is the number of edges; space complexity is O(N) due to the queue and visited array.
• 🔁 BFS traversal order depends on the starting node, and different starting points can produce different level structures.
• 📚 Understanding BFS is crucial before tackling other graph algorithms like DFS (Depth First Search), which is typically learned next.

Q & A

What is Breadth First Search (BFS)?

BFS is a graph traversal technique that explores a graph level by level, starting from a given node. It uses a queue to ensure nodes are explored in a breadth-wise manner.

How does BFS differ from Depth First Search (DFS)?

BFS explores a graph level by level, whereas DFS explores as deep as possible along a branch before backtracking. BFS uses a queue, while DFS uses a stack or recursion.

What is the significance of 'breadth' in BFS?

The term 'breadth' in BFS refers to the way the algorithm explores nodes level by level, starting from the root node and moving outwards.

What data structures are used in BFS?

BFS uses two main data structures: a queue (for storing nodes to be explored) and a visited array (to track nodes that have been processed).

What does the visited array do in BFS?

The visited array keeps track of which nodes have already been explored to prevent revisiting them, ensuring each node is processed only once.

Why is it important to handle different graph indexing types in BFS?

Graphs can be indexed either from 0 or 1. It's important to account for this in your code to ensure the visited array and adjacency list are set up correctly based on the graph's indexing type.

How is the BFS traversal order determined?

The order of traversal in BFS is determined by the level of each node, starting from the source node. All neighbors at the same level are explored before moving to the next level.

Can BFS work with both directed and undirected graphs?

Yes, BFS works with both directed and undirected graphs. In undirected graphs, each edge is bidirectional, while in directed graphs, traversal follows the direction of edges.

How does the starting node affect BFS traversal?

The starting node sets the beginning of the BFS traversal. Depending on the starting node, the BFS traversal order can differ as different paths are explored first.

What is the time complexity of BFS?

The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges. Each node is processed once, and each edge is explored once.