Aula 3.5 - Teorema de Helmholtz e Exercícios
Summary
TLDRThe script delves into Maxwell's equations, explaining the divergence and curl of electric and magnetic fields, and their significance in electromagnetism. It introduces counterexamples to Helmholtz's theorem, emphasizing the importance of boundary conditions in field definition. Practical problems are presented, such as calculating the divergence of a vector field and applying the divergence theorem to verify flux calculations. The lecture highlights the relevance of these concepts in understanding electromagnetic theory and provides step-by-step guidance on solving related problems in cylindrical coordinates.
Takeaways
- 😀 Helmholtz's theorem relates to defining fields based on their divergence and curl, but additional information, such as boundary conditions, is also necessary.
- 😀 A counterexample was presented showing that a field with zero divergence and zero curl doesn't necessarily violate Helmholtz's theorem, but the boundary condition must be considered.
- 😀 The divergence of a field is the sum of the derivatives of its components with respect to spatial coordinates.
- 😀 A completely uniform, constant field has both zero divergence and zero curl, but it still needs boundary conditions to be fully defined.
- 😀 Helmholtz's theorem ensures that, given the divergence, curl, and boundary conditions, a field can be uniquely determined.
- 😀 The divergence theorem was applied to check the consistency between the surface flux and volume integral of a vector field.
- 😀 The volume of a 1/4-cylinder (height 5, radius 2) was calculated, and this was used to verify the divergence theorem with a result of 40 pi.
- 😀 The flux through various surfaces of a cylinder was calculated, including the top, bottom, and side surfaces, with certain integrals yielding zero flux due to symmetry.
- 😀 The curl of a vector field in cylindrical coordinates was calculated, and in this case, the result was zero, demonstrating that the rotational component of the field is zero.
- 😀 Various integrals and surface calculations in cylindrical coordinates were shown, illustrating how divergence and curl computations are done in electromagnetism.
Q & A
What is the purpose of Maxwell's equations in electromagnetism?
-Maxwell's equations are fundamental to the theory of electromagnetism, as they describe how electric and magnetic fields are generated and altered by each other and by charges and currents. They are essential for understanding the behavior of electromagnetic waves, which include light.
What are the key components of Maxwell's equations discussed in the transcript?
-The transcript discusses two equations for the electric field and two for the magnetic field, focusing on the divergence and curl of these fields. The divergence refers to the net flow out of a point, while the curl relates to the rotation of the field at a point.
What is the significance of divergence and curl in field theory?
-Divergence and curl are key operations in vector calculus that help describe the behavior of fields. Divergence quantifies the 'spread' or 'convergence' of a field, while curl measures the rotation or circulation of a field at a point. These concepts are central to Maxwell's equations and electromagnetic theory.
What counterexamples were provided to illustrate Helmholtz's theorem?
-The transcript presents two counterexamples: a uniform constant field and a function where the divergence and curl are both zero. These counterexamples show that Helmholtz's theorem, which connects the divergence and curl of a field with its uniqueness, must also include the boundary conditions (contour) for the field to be fully defined.
What is Helmholtz's theorem and why is it important?
-Helmholtz's theorem states that if the divergence, curl, and boundary conditions of a field are known, the field is completely determined. This theorem is crucial in electromagnetism because it ensures the uniqueness of solutions for fields based on these properties, assuming proper boundary conditions are applied.
What does the contour condition refer to in Helmholtz's theorem?
-The contour condition refers to the requirement that the field must approach zero at infinity (or within a specific region). This boundary condition ensures that the field is well-behaved and uniquely determined, preventing non-physical solutions such as fields that do not decay at large distances.
How is the divergence of the field calculated in the transcript?
-The divergence is calculated by applying the definition of divergence in spherical coordinates. The given field involves terms dependent on the radial coordinate 's' and the angular coordinate 'phi.' The derivatives of these terms are computed with respect to 's,' 'phi,' and 'z' to obtain the total divergence.
What is the divergence theorem and how is it verified in the transcript?
-The divergence theorem relates the flux of a vector field through a closed surface to the volume integral of the field's divergence. In the transcript, the flux is calculated over the surface of a 1/4-cylinder, and the volume integral is computed. Both calculations yield the same result, verifying the validity of the divergence theorem.
What steps are involved in calculating the flux on the surface of the cylinder?
-To calculate the flux, the surface integral of the vector field is computed over each part of the cylinder's surface: the top, the bottom, and the side faces. The contributions from the top and bottom surfaces are zero due to the nature of the field, while the side surfaces are evaluated using the correct area elements and integrals.
What is the result of calculating the curl of the field as shown in the transcript?
-The curl of the given vector field is calculated to be zero. This is demonstrated by applying the cylindrical coordinate expressions for curl and differentiating the components of the field with respect to the relevant variables. The terms cancel out, leading to a zero curl, indicating no rotation in the field.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

LISTRIK MAGNET 14 2 Penurunan persamaan Maxwell serta arti fisis Arus Perpindahan
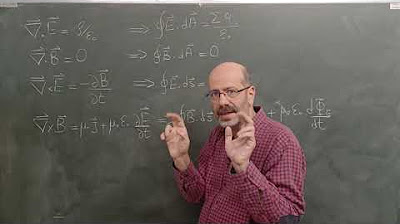
Maxwell Denklemleri Ne Anlama Gelir?

El Campo Electromagnético, cómo surgen las fuerzas Eléctricas y Magnéticas

This Downward Pointing Triangle Means Grad Div and Curl in Vector Calculus (Nabla / Del) by Parth G

Maxwell's Contributions to Electromagnetism // HSC Physics

A Lei de Ampère-Maxwell: Campos elétricos induzem campos magnéticos.
5.0 / 5 (0 votes)
