Espacios de coordenadas reales
Summary
TLDREste video explica de manera clara y accesible los conceptos de espacios coordenados reales, comenzando con R2 (espacio bidimensional) y extendiéndolos a R3 (espacio tridimensional) y más allá a espacios de n dimensiones. A través de ejemplos prácticos con vectores y tuplas, se ilustra cómo estos espacios están formados por combinaciones de números reales, y se discute la importancia de la notación matemática, como R2 y R3, para representar estas dimensiones. El video también destaca cómo podemos trabajar con dimensiones superiores, a pesar de que no sea posible visualizarlas, utilizando herramientas matemáticas como los vectores y matrices.
Takeaways
- 😀 La notación R² representa el espacio de dos dimensiones con coordenadas reales, es decir, el espacio en el que ya estamos acostumbrados a trabajar.
- 😀 R² se refiere a todas las combinaciones posibles de coordenadas reales con dos entradas, conocidas como dos tuplas.
- 😀 Un vector en R² se representa como una dos tupla de valores reales, como por ejemplo (3, 4), donde el orden de los valores importa.
- 😀 Las combinaciones posibles de dos tuplas con valores reales forman el espacio de dos dimensiones R².
- 😀 El concepto de un vector también se aplica en R², donde cada vector tiene dirección y magnitud, y no necesariamente debe salir del origen.
- 😀 R³ es el espacio de tres dimensiones con coordenadas reales, que se representa como todas las posibles tres tuplas con valores reales.
- 😀 En R³, un ejemplo de vector podría ser (0, 0, 0) o (-1, 5, 3), los cuales son elementos de R³.
- 😀 Un elemento de R³ debe ser una tres tupla con valores reales, mientras que una dos tupla pertenece a R².
- 😀 Cualquier tupla que contenga números imaginarios no pertenece a R³, ya que no cumple con la condición de tener solo valores reales.
- 😀 Aunque es difícil de visualizar, es posible trabajar con espacios de más dimensiones, como R⁴, R⁵ o incluso Rⁿ, donde n puede ser cualquier número, representando un espacio n-dimensional con coordenadas reales.
Q & A
¿Qué significa la notación con la R doble línea en el contexto de las matemáticas?
-La notación R con doble línea representa el espacio de dos dimensiones con coordenadas reales. Es un espacio matemático en el cual las coordenadas son números reales en dos dimensiones.
¿Cuál es la diferencia entre R2 y la notación R2 con el exponente 2?
-R2 es el espacio de dos dimensiones con coordenadas reales, mientras que el exponente 2 (como en R^2) simplemente indica que estamos trabajando en un espacio bidimensional.
¿Qué significa que el espacio R2 sea el 'espacio de dos dimensiones con coordenadas reales'?
-Esto se refiere a que el espacio está formado por todas las combinaciones posibles de dos números reales, es decir, las posibles tuplas ordenadas de dos valores reales.
¿Cómo se representa un vector en R2?
-Un vector en R2 se representa como una tupla ordenada de dos números reales. Por ejemplo, un vector podría ser (3, 4) o (-3, -4), donde los números representan las coordenadas en los ejes X e Y, respectivamente.
¿Por qué el orden de los números en una tupla de R2 es importante?
-El orden es importante porque las tuplas ordenadas, como (3, 4) y (4, 3), representan puntos diferentes en el plano. El primer número se refiere a la coordenada en el eje horizontal y el segundo en el eje vertical.
¿Qué representa el vector (0, 0) en R2?
-El vector (0, 0) en R2 es el vector nulo, el cual no tiene magnitud ni dirección, ya que está en el origen del espacio bidimensional.
¿Cómo se define R3 en matemáticas?
-R3 es el espacio tridimensional con coordenadas reales. Es un espacio formado por todas las posibles tuplas ordenadas de tres números reales, representando coordenadas en tres dimensiones.
¿Qué ejemplo se da en el video de un vector en R3?
-Un ejemplo dado es el vector (-1, 5, 3), que pertenece a R3 porque es una tupla de tres valores reales que representa un punto en un espacio tridimensional.
¿Qué significa que un vector con entradas imaginarias no pertenezca a R3?
-Un vector con entradas imaginarias, como (i, 0, 1), no pertenece a R3 porque las coordenadas no son números reales. Las coordenadas en R3 deben ser exclusivamente números reales.
¿Qué es Rn y cómo se define?
-Rn es el espacio de n dimensiones con coordenadas reales, donde 'n' puede ser cualquier número entero positivo. Es un espacio abstracto que generaliza los espacios de 2, 3, o más dimensiones, y se puede visualizar matemáticamente aunque no sea posible representarlo físicamente.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

SUBESPACIOS Vectoriales | 2 Ejercicios RESUELTOS

Una comprensión más formal de las funciones

Zona RURAL y URBANA 🤓 | Características del campo 🏞️ y la ciudad 🏙️
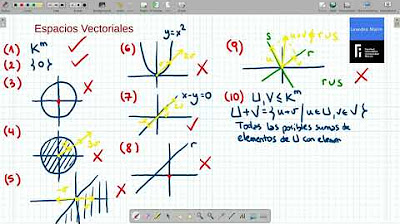
AMD T11 - Espacios Vectoriales

😉 OpenToonz Tutorial English ▶ User Interface #03

Simulacion 2D en Python - Parte 1 Intro- Como Programar Universo con Fuerzas
5.0 / 5 (0 votes)
