Sifat-Sifat Dua Segitiga Sebangun
Summary
TLDRIn this lesson for ninth-grade students, the teacher explains the properties of similar triangles, focusing on angle-angle similarity (AA), side-side-side (SSS), and side-angle-side (SAS) similarity. The lesson includes clear examples and step-by-step explanations on how to identify and prove that two triangles are similar based on these properties. Students are encouraged to engage with visual aids, solve practice problems, and access further exercises through Google Classroom. The teacher concludes with a preview of the next topic on congruent triangles, aiming to reinforce students' understanding and application of geometric concepts.
Takeaways
- 😀 The lesson is about learning the properties of similar triangles.
- 😀 The video starts with a warm greeting and encourages students to stay healthy and motivated while learning from home.
- 😀 The importance of subscribing to the channel is emphasized to motivate the teacher to create more educational content.
- 😀 The lesson will explain how to distinguish between congruent and similar triangles, based on their angles and sides.
- 😀 The first property of similar triangles is that corresponding angles are equal (SDS - Side-Angle-Side).
- 😀 The second property is that the corresponding sides of similar triangles are proportional (SSS - Side-Side-Side).
- 😀 The third property is that two angles of one triangle are congruent to two angles of another triangle, and the included sides are proportional (SAS - Side-Angle-Side).
- 😀 Example problems are used to demonstrate how these properties are applied to prove whether two triangles are similar.
- 😀 A detailed explanation of how to compare angles and sides using specific notations and symbols is provided.
- 😀 The video concludes with a reminder to complete exercises in Google Classroom and prepare for the next lesson on congruent triangles.
Q & A
What are the three properties of similar triangles discussed in the video?
-The three properties of similar triangles discussed are: 1) Angle-Angle-Angle (AAA) or Triple SD, where the angles of two triangles are the same; 2) Side-Side-Side (SSS) or Triple S, where the corresponding sides of the triangles are proportional; and 3) Side-Angle-Side (SAS) or SDS, where one angle is the same and the sides enclosing the angle are proportional.
What is the purpose of the 'Triple SD' property in identifying similar triangles?
-'Triple SD' (Angle-Angle-Angle or AAA) property helps identify similar triangles by confirming that if all corresponding angles of two triangles are equal, the triangles are similar.
How do we determine if two triangles are similar using the 'Triple S' property?
-To determine if two triangles are similar using the 'Triple S' (Side-Side-Side) property, we check if the corresponding sides of the two triangles are proportional. If the ratio of the corresponding sides is the same, the triangles are similar.
What does the 'Side-Angle-Side' (SAS) property indicate for two triangles?
-The 'Side-Angle-Side' (SAS) property indicates that if one angle of two triangles is equal and the sides enclosing that angle are proportional, then the two triangles are similar.
In the example of triangle ABC and DEF, how do we prove they are similar?
-In the example of triangle ABC and DEF, we prove they are similar by showing that their corresponding angles are equal, and their sides are proportional. Specifically, the angles A, B, and C correspond to angles D, E, and F, and the sides AB, BC, and CA correspond to sides DE, EF, and FD.
How do we prove that two triangles are similar using side proportions?
-To prove two triangles are similar using side proportions, we compare the lengths of the corresponding sides. If the ratios of the corresponding sides are equal, the triangles are similar. This is known as the Side-Side-Side (SSS) property.
Why is it important to check both angles and sides when determining if triangles are similar?
-It is important to check both angles and sides when determining if triangles are similar because similarity is based on either equal angles (Angle-Angle-Angle or AAA) or proportional sides (Side-Side-Side or SSS), or a combination of both (Side-Angle-Side or SAS). This ensures that the triangles share the same shape, regardless of size.
What is the significance of using symbols like circles, X, and stars to mark angles in the video?
-The use of symbols like circles, X, and stars to mark angles in the video helps to visually indicate which angles are congruent (i.e., have the same measure) in the two triangles, making it easier to identify corresponding angles for comparison.
In the video, what is the first step in proving that two triangles are similar?
-The first step in proving that two triangles are similar is to identify the corresponding angles or sides and check if they are either equal or proportional. For example, in the case of triangle ABC and DEF, we start by comparing their angles.
What is the relationship between 'congruent triangles' and 'similar triangles' as discussed in the video?
-The video explains that congruent triangles are a specific type of similar triangles where both their corresponding angles and sides are exactly equal. In contrast, similar triangles only need to have equal angles and proportional sides, but they do not need to be of the same size.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

⭕ Semelhança de Triângulos - GEOMETRIA PLANA (Aula 12)

Semelhança de Triângulos - Professora Angela

CRITERIOS de CONGRUENCIA de Triángulos | Desde Cero
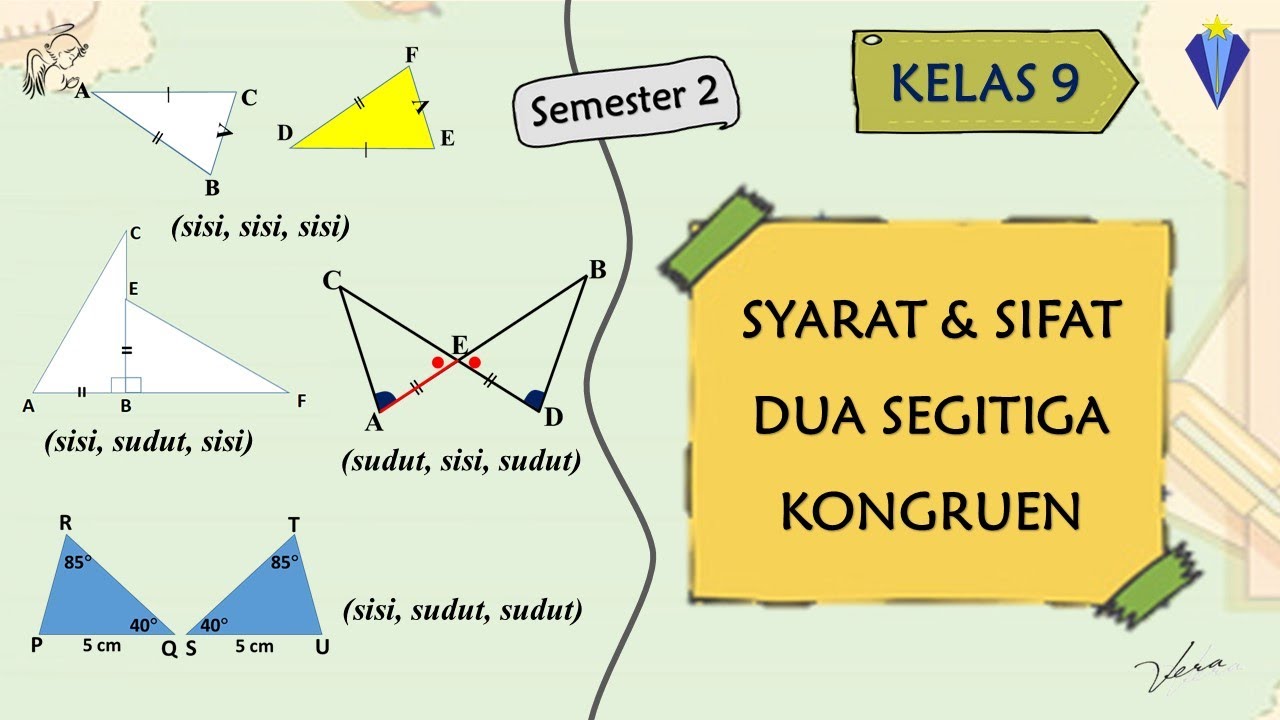
2 SYARAT DAN SIFAT DUA SEGITIGA KONGRUEN - KESEBANGUNAN DAN KONGRUENSI - KELAS 9 SMP

Triangle Congruence Theorems Explained: ASA, AAS, HL

Kesebangunan & Kongruensi (6) - Rumus Kongruensi, Pembuktian Kongruensi - Matematika SMP
5.0 / 5 (0 votes)
