The Continuity Equation

Summary

In this video, the speaker explores the principle of continuity in fluid dynamics, focusing on conservation of mass and volume. By using the ocean as a model, they demonstrate how mass entering and exiting a system must remain equal, leading to the conservation of volume. The speaker breaks down key concepts such as density, volume transport, and velocity, and derives the continuity equation: ∂u/∂x + ∂v/∂y + ∂w/∂z = 0. They explain the equation's importance in understanding fluid flow and use a 'chewing gum' analogy to help visualize how water parcels behave when compressed or stretched in different directions.

Takeaways

• 😀 Continuity is based on the concept of conservation of mass and volume, meaning that mass (and volume) cannot be created or destroyed.
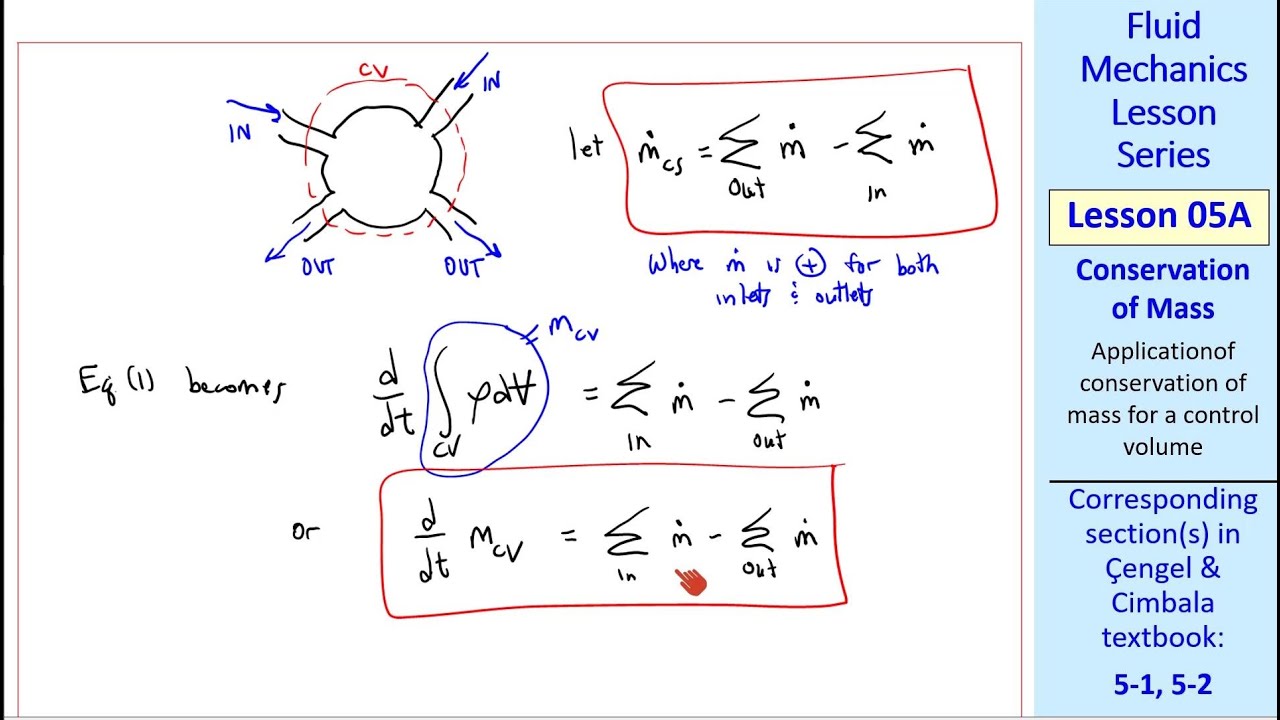
• 😀 In a closed system, the rate of mass flowing in must equal the rate of mass flowing out, maintaining conservation of mass.
• 😀 Density (ρ) is a key factor in the calculation of mass, as mass is equal to density times volume (M = ρ × V).
• 😀 The Boussinesq approximation simplifies calculations by assuming changes in density are negligible, allowing the equation to focus on volume alone.
• 😀 The principle of continuity in a fluid system suggests that the volume transport in must equal the volume transport out.
• 😀 Volume transport is calculated by multiplying the velocity of the fluid by the area through which it flows.
• 😀 The continuity equation is derived from the conservation of volume, and is written as ∂u/∂x + ∂v/∂y + ∂w/∂z = 0.
• 😀 The continuity equation ensures that changes in fluid velocity in one direction must be balanced by changes in other directions to conserve volume.
• 😀 A simple analogy for the continuity equation is thinking of a parcel of water as chewing gum—stretching it in one direction causes it to thin out in others.
• 😀 The continuity equation is crucial for analyzing fluid flow in complex systems like the ocean, where volume must be conserved in all directions.

Q & A

What is the concept of continuity in the context of fluid dynamics?

Continuity refers to the idea that a fluid, such as the ocean, is continuous with no gaps or holes in it. This principle is analogous to the conservation of mass, where mass is neither created nor destroyed, but it extends to conservation of volume in fluid systems.

How does conservation of mass relate to the principle of continuity?

Conservation of mass states that the mass entering a system must equal the mass exiting it. In the case of the ocean, this concept is extended to volume conservation, implying that the volume of water entering a region must equal the volume exiting it, thus maintaining continuity.

What does the term 'mass transport' mean in the context of the ocean?

Mass transport refers to the movement of mass into or out of a system. In the ocean, mass transport is determined by the water's density (ρ) and the volume (V) it occupies, meaning mass transport is the product of density and volume.

What is the formula for mass and how is it applied in the conservation of mass?

Mass is calculated as the product of density (ρ) and volume (V). This formula is used in the conservation of mass to ensure that the mass flowing into a system is equal to the mass flowing out.

How is volume transport related to velocity and area?

Volume transport is the product of velocity and area. In fluid dynamics, volume transport represents the amount of fluid (or water in this case) flowing through a given area per unit of time. The formula for volume transport is volume per time (m³/s), which is the velocity (m/s) times the cross-sectional area (m²).

What does the continuity equation represent?

The continuity equation represents the conservation of volume in a fluid system. It ensures that the rate at which volume enters a system equals the rate at which volume exits. Mathematically, it is expressed as ∂u/∂x + ∂v/∂y + ∂w/∂z = 0, where u, v, and w are the velocities in the X, Y, and Z directions respectively.

Why is the continuity equation important in fluid dynamics?

The continuity equation is fundamental because it governs the behavior of fluids in a system. It ensures that the volume of fluid remains constant despite changes in velocity or direction, making it crucial for understanding fluid flow in oceans, pipes, and other systems.

How does the continuity equation account for changes in velocity?

The continuity equation accounts for changes in velocity by ensuring that any increase in velocity in one direction must be compensated by changes in velocity in other directions. This is consistent with the physical principle that the total volume flow remains conserved.

What is the physical interpretation of the continuity equation in the context of ocean water flow?

The physical interpretation is that if the velocity of water increases in one direction (e.g., the X-direction), the water must spread out or decrease in velocity in other directions (e.g., Y or Z), ensuring the volume of water is conserved as it moves through the system.

What is the 'Boussinesq approximation' mentioned in the script?

The Boussinesq approximation assumes that density changes in the ocean are negligible and can be ignored in most fluid dynamics problems. This simplifies the continuity equation by ignoring small variations in density that have minimal impact on volume transport.