part 1 materi irisan kerucut parabola kelas 12 materi kelas 12 kurikulum merdeka geometri analitik
Summary
TLDRIn this video, the speaker covers various equations of parabolas, focusing on their general forms such as x² = 4py, x² = -4py, y² = 4px, and y² = -4px. The video explains the characteristics of each parabola, such as their direction of opening (up, down, left, right), vertex, focus, directrix, and length of the latus rectum. Additionally, it dives into the formulas for tangent lines at specific points and offers step-by-step solutions to problems involving parabola equations. Viewers will gain a comprehensive understanding of parabola properties and how to work with them in mathematical contexts.
Takeaways
- 😀 Parabolas can be categorized by their equations: x^2 = 4py, x^2 = -4py, y^2 = 4px, and y^2 = -4px, each representing different orientations of the curve.
- 😀 The vertex of a parabola defined by x^2 = 4py is at (0, 0), and its focus is located at (0, p), with the directrix parallel to the x-axis at y = -p.
- 😀 For the equation x^2 = -4py, the parabola opens downward, with the focus at (0, -p) and the directrix at y = p.
- 😀 The general equation y^2 = 4px represents a parabola that opens to the right, with the focus at (p, 0) and the directrix at x = -p.
- 😀 For y^2 = -4px, the parabola opens to the left, with the focus at (-p, 0) and the directrix at x = p.
- 😀 The equation for the tangent to a parabola at a given point (x1, y1) is derived using the formula y * y1 = 2p * (x + x1), with a specific form for the gradient.
- 😀 To find the equation of the tangent line through a specific point on the parabola, use the general tangent formula y = mx + p/m, where m is the slope at the point.
- 😀 In practice, when working with specific problems, determining the value of p (the distance from the vertex to the focus or directrix) is crucial for defining the parabola.
- 😀 Example problems involve finding the equation of a parabola from given focus coordinates or directrix, using the standard forms based on whether the parabola opens up, down, left, or right.
- 😀 Parabola problems can also involve finding the equation of the tangent line to the curve at specific points, requiring the application of the tangent formula and gradient calculations.
Q & A
What are the general equations of a parabola discussed in the video?
-The general equations discussed are: x^2 = 4py (opens upwards), x^2 = -4py (opens downwards), y^2 = 4px (opens to the right), and y^2 = -4px (opens to the left).
How is the focus of a parabola determined for the equation x^2 = 4py?
-For the equation x^2 = 4py, the focus is located at the point (0, p), where p is the distance from the vertex (0, 0) along the y-axis.
What is the equation of the directrix for the parabola x^2 = 4py?
-The equation of the directrix for x^2 = 4py is y = -p, which is parallel to the x-axis and located at a distance p below the vertex.
How is the equation of a tangent line to a parabola derived from its general equation?
-The tangent line at a point (x1, y1) on the parabola is derived by using the formula: y * y1 = (x - x1) * (2p) or similar forms depending on the specific parabola equation.
In the equation y^2 = 4px, how can you find the focus and directrix?
-For the equation y^2 = 4px, the focus is at (p, 0) and the directrix is at x = -p. This equation represents a parabola that opens to the right.
How is the value of p used to determine the shape and direction of a parabola?
-The value of p determines the orientation and width of the parabola. A positive p value opens the parabola upwards (for x^2 = 4py) or to the right (for y^2 = 4px), while a negative p value opens the parabola downwards (for x^2 = -4py) or to the left (for y^2 = -4px).
How is the length of the latus rectum determined for a parabola?
-The length of the latus rectum is given by the formula 4|p|, where p is the distance from the vertex to the focus. This length remains constant for any given parabola.
What does the term 'symmetric axis' mean in the context of parabolas?
-The symmetric axis of a parabola is the line that passes through its vertex and focus, dividing the parabola into two symmetric halves. For parabolas like x^2 = 4py or y^2 = 4px, the axis is either the y-axis or the x-axis, respectively.
How would you solve for the equation of a parabola if given the focus and directrix?
-To solve for the equation of a parabola given the focus and directrix, first identify the vertex's position (midpoint between focus and directrix). Then, use the general equation for the corresponding parabola type, substituting the known values for p, the focus coordinates, and the directrix.
What is the significance of the absolute value of p in determining the parabola's properties?
-The absolute value of p determines the distance between the vertex and the focus, and it is used to calculate the length of the latus rectum. The sign of p (positive or negative) dictates whether the parabola opens upwards, downwards, left, or right.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
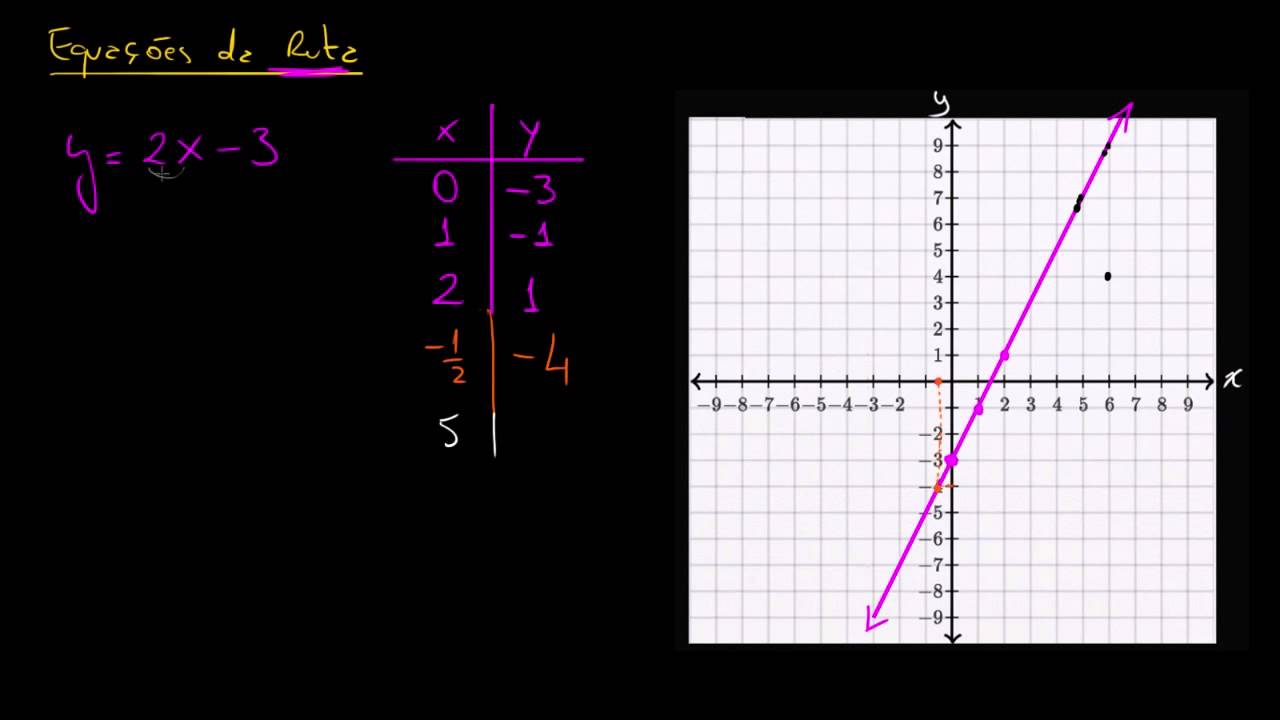
Equações lineares com duas variáveis e seus gráficos

Pengertian Kemiringan Hal 235-238 Bab 5 Persamaan Garis Lurus Kelas 8 Kurikulum Merdeka Belajar

Massive New Study shows Niacin and NAD+ cause Heart Disease?? Is this true? [Study 282]

Linear Equations - Algebra
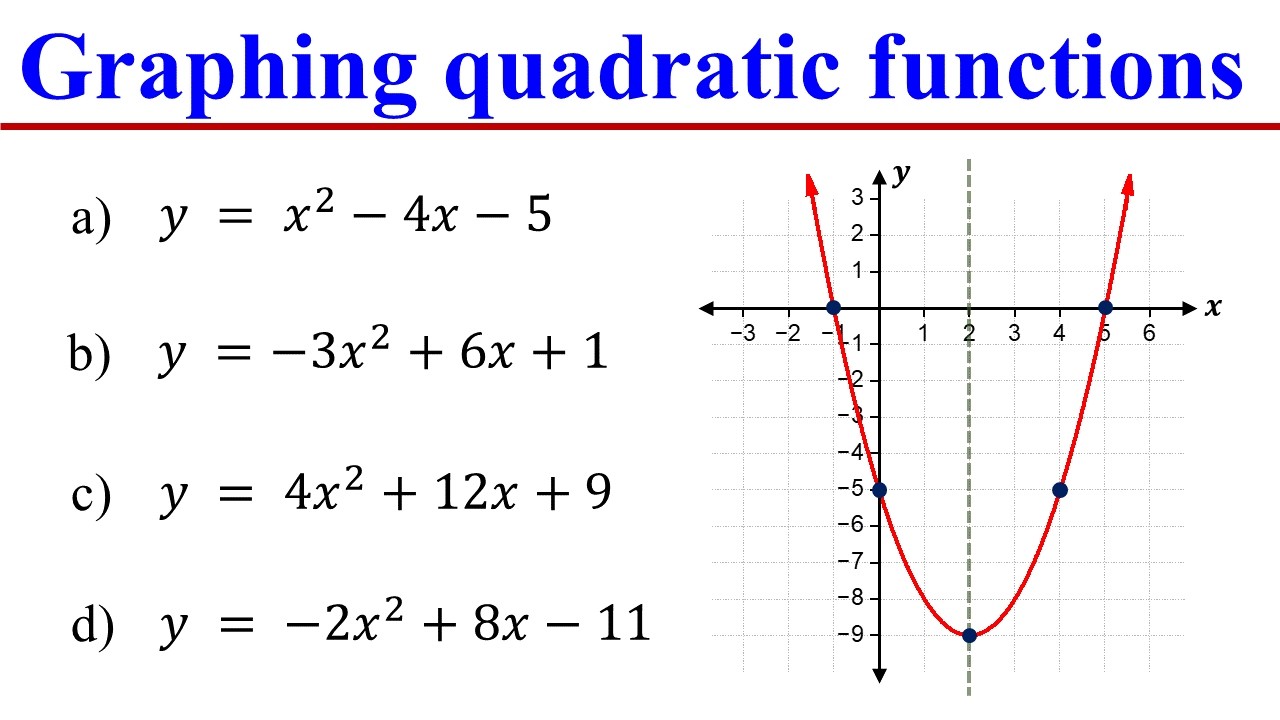
How to Graph Quadratic Functions by finding the Vertex, Axis of symmetry, X & Y intercepts
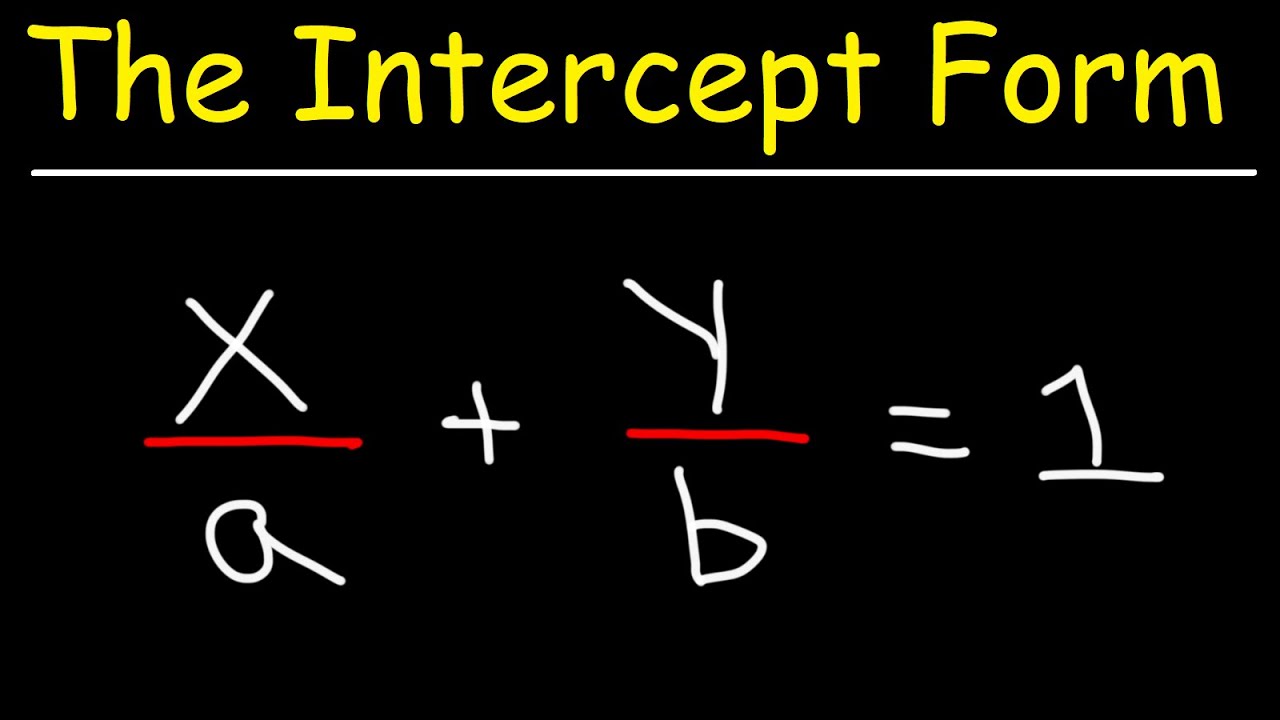
Linear Equations - The Intercept Form - Algebra
5.0 / 5 (0 votes)
