Common Big O Runtimes

Summary

This video introduces common Big-O run times, explaining their significance in analyzing algorithm efficiency. It covers five key complexities: O(log n), O(n), O(n log n), O(n²), and O(n!), providing examples such as binary search, linear search, quicksort, selection sort, and the traveling salesman problem. The video visually demonstrates how these complexities grow with different input sizes (n = 10, 20, 100), highlighting how factorial time (O(n!)) increases drastically, making certain problems practically unsolvable. The video concludes by emphasizing the importance of understanding these complexities for optimizing algorithms.

Takeaways

• 😀 Big-O notation helps analyze the time complexity of algorithms, showing how the execution time increases with input size.
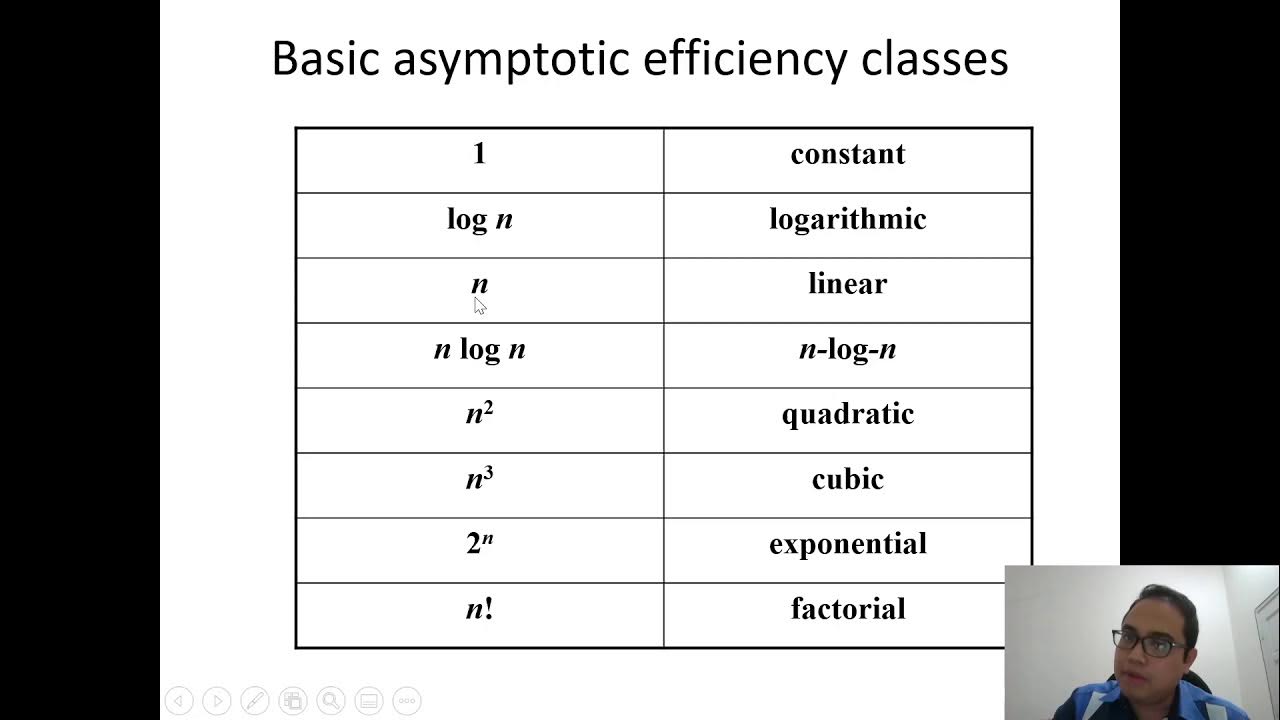
• 😀 Common Big-O run times include O(log n), O(n), O(n log n), O(n²), and O(n!).
• 😀 O(log n), also known as logarithmic time, represents algorithms like Binary Search, which are efficient even for large datasets.
• 😀 O(n), or linear time, is the complexity of algorithms like Linear Search, where the execution time grows directly with the input size.
• 😀 O(n log n) is a combination of linear and logarithmic growth, and it's the complexity of fast sorting algorithms like Quick Sort.
• 😀 O(n²), or quadratic time, is seen in algorithms like Selection Sort, which perform poorly as the input size increases.
• 😀 O(n!) represents exponential growth and is the time complexity of problems like the Traveling Salesman Problem, making such problems computationally expensive.
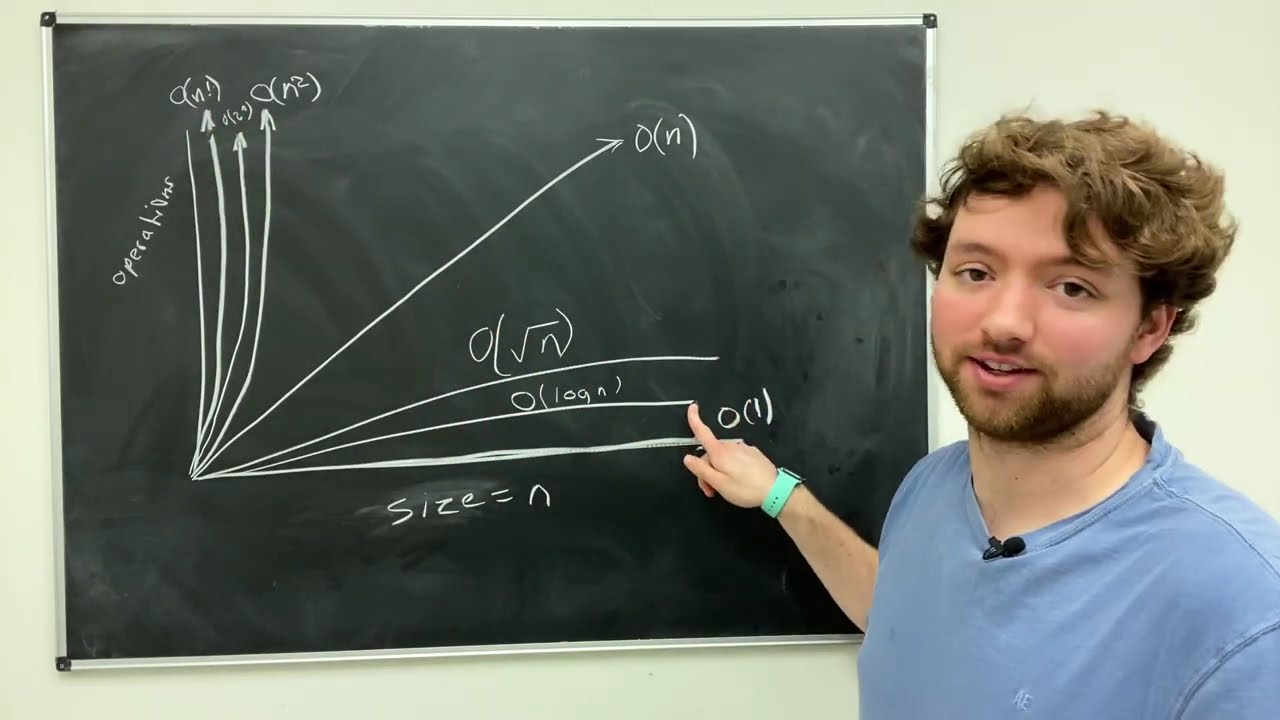
• 😀 Visualization of these complexities helps compare how the number of operations increases with different input sizes, illustrating their growth patterns.
• 😀 As the input size (n) increases, the growth rate of O(n!) becomes drastically large compared to other complexities like O(log n) and O(n).
• 😀 The order of growth for common complexities is: O(log n) < O(n) < O(n log n) < O(n²) < O(n!). This hierarchy helps identify which algorithms are more efficient.
• 😀 Even for smaller inputs, algorithms with factorial time complexity (O(n!)) like the Traveling Salesman Problem can have infeasible computation times.

Q & A

What is Big-O notation?

Big-O notation is a way of expressing the time complexity of an algorithm, showing how the number of operations required grows as the input size increases. It provides an upper bound on the running time of an algorithm.

What does a time complexity of O(log n) mean?

A time complexity of O(log n) means that the number of operations grows logarithmically with the input size. As the input size increases, the algorithm's growth rate increases slowly. An example is binary search.

Why is binary search considered one of the fastest algorithms?

Binary search is considered one of the fastest algorithms because it operates in O(log n) time. It efficiently searches through a sorted list by repeatedly halving the search space, making it very efficient even for large input sizes.

What does a time complexity of O(n) mean?

A time complexity of O(n) means that the number of operations increases linearly with the input size. Each additional element in the input requires one additional operation. Linear search is an example of an algorithm with O(n) time complexity.

What is the difference between O(n) and O(n log n) time complexity?

O(n) is linear time, where the number of operations grows directly with the input size, while O(n log n) is log-linear time, where the growth rate is a combination of linear growth and logarithmic growth. O(n log n) is typically seen in more efficient sorting algorithms like quicksort.

Why is quicksort considered efficient?

Quicksort is considered efficient because it operates in O(n log n) time, which is faster than O(n²) algorithms like selection sort. It uses a divide-and-conquer approach to sort elements quickly.

What is the significance of O(n²) time complexity?

O(n²) time complexity indicates quadratic growth, where the number of operations grows as the square of the input size. This is typical of algorithms like selection sort, which becomes inefficient for large data sets.

Why is O(n!) time complexity considered exponential?

O(n!) time complexity is considered exponential because the number of operations grows very rapidly as the input size increases. Even for small input sizes, the number of operations can become unmanageable. The traveling salesman problem is an example of a problem with O(n!) complexity.

What is the relationship between different Big-O complexities?

The different Big-O complexities can be ordered by their growth rates: O(log n) is the slowest, followed by O(n), O(n log n), O(n²), and O(n!) which grows the fastest. This means that for large inputs, algorithms with lower Big-O complexities are more efficient.

What practical insight can be gained from the table showing different Big-O complexities?

The table shows that as input size increases, the number of operations grows at different rates depending on the algorithm's time complexity. For example, even for relatively small inputs, O(n!) algorithms like the traveling salesman problem can require impractically long computation times, illustrating why such problems are considered undecidable.