Irisan Kerucut Matematika Kelas 11 • Part 1: Macam-Macam (Lingkaran, Parabola, Elips, Hiperbola)
Summary
TLDRThis video explores the different types of conic sections formed when a cone is intersected by a plane: circles, ellipses, parabolas, and hyperbolas. The shapes that emerge depend on the angle at which the plane intersects the cone and whether it passes through the cone's apex. The video explains how the geometry changes with varying angles (alpha and beta), illustrating each shape’s characteristics. The presenter focuses on understanding the relationships between the cone’s axis, the plane, and the resulting conic sections, providing a clear, accessible explanation for viewers.
Takeaways
- 😀 Conic sections occur when a cone is intersected by a flat plane, and the resulting shapes can be a circle, point, ellipse, parabola, hyperbola, or a pair of straight lines.
- 😀 The shapes formed depend on the orientation and angle of the intersecting plane relative to the cone.
- 😀 A circle is formed when the intersecting plane is perpendicular to the axis of the cone and does not pass through the cone's apex.
- 😀 If the intersecting plane is horizontal and passes through the apex, the result is a point, not a circle.
- 😀 A parabola is formed when the plane cuts the cone in a direction parallel to the slant height of the cone, with specific conditions about the angles.
- 😀 The angles involved in forming a parabola include the angle between the cone's axis and the plane, which should be equal to the angle between the cone's slant height and the plane.
- 😀 An ellipse forms when the intersecting plane cuts through the cone at an angle greater than that of a parabola, but not passing through the apex.
- 😀 For an ellipse, the angle between the plane and the cone's axis (alpha) is greater than the angle between the slant height and the axis (beta).
- 😀 A hyperbola is created when the angle between the plane and the cone's axis is smaller than the angle between the slant height and the axis.
- 😀 If a hyperbola’s plane passes through the apex of the cone, the result is two intersecting straight lines, not a hyperbola.
- 😀 In summary, the four main types of conic sections (circle, parabola, ellipse, hyperbola) are determined by the relationship between the angles alpha and beta, and whether the plane passes through the apex of the cone.
Q & A
What are the five types of conic sections discussed in the video?
-The five types of conic sections discussed are: circle, point, ellipse, parabola, and hyperbola.
What condition results in the conic section being a circle?
-A circle is formed when the cutting plane is perpendicular to the axis of the cone, and it does not pass through the apex.
When does the intersection of the cone and the plane form a parabola?
-A parabola forms when the cutting plane is parallel to one of the slant heights of the cone and does not pass through the apex.
What is the difference between an ellipse and a parabola in terms of the cutting plane's angle?
-An ellipse forms when the cutting plane’s angle (alpha) is greater than the angle between the slant height and the axis (beta), whereas a parabola forms when alpha equals beta.
How is a hyperbola formed in conic section theory?
-A hyperbola is formed when the cutting plane's angle (alpha) is smaller than the angle between the slant height and the axis (beta), and the plane does not pass through the apex of the cone.
What happens if the cutting plane passes through the apex of the cone?
-If the cutting plane passes through the apex of the cone, the result is not a conic section like a circle, ellipse, or parabola. Instead, it may result in a point (in the case of a circle) or a pair of straight lines (in the case of a hyperbola).
What does the term 'alpha' (α) represent in the context of conic sections?
-Alpha (α) represents the angle between the cutting plane and the axis of the cone (the vertical line that defines the cone's height).
What is the significance of the 'beta' (β) angle in forming conic sections?
-Beta (β) is the angle between the cutting plane and the slant height of the cone, which affects the shape of the resulting conic section.
Why does a hyperbola form when the angle alpha is less than beta?
-A hyperbola forms when alpha is less than beta because the plane cuts through the cone at a sharper angle, creating two distinct curves that open away from each other, resulting in a hyperbola.
What happens to the conic section if the cutting plane is shifted so that it passes through the apex of the cone?
-If the cutting plane passes through the apex of the cone, the conic section can collapse into a point (circle) or form straight lines (hyperbola), rather than forming typical curves like circles, ellipses, or parabolas.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

What are Conic Sections? | Don't Memorise

Intro to Conic Sections | Pre Calculus | STEM Math
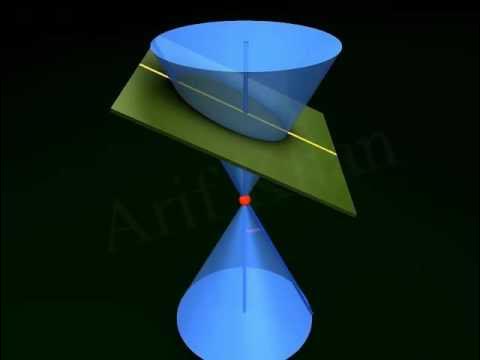
Conic Section 3D Animation
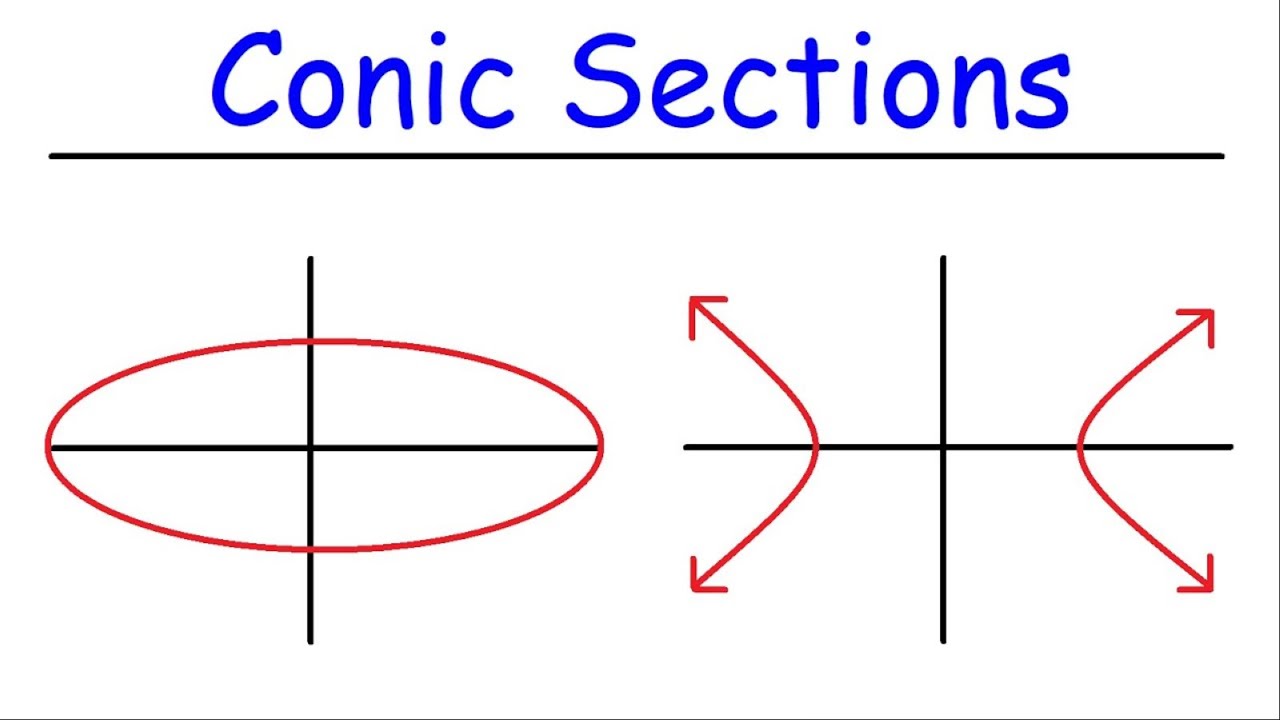
Conic Sections - Circles, Semicircles, Ellipses, Hyperbolas, and Parabolas

Conic Section 3D Animation | explain conic section one shot | hyperbola and parabola

SHS Pre-calculus Q1 Ep1: Introduction to Pre-calculus and Conic Sections
5.0 / 5 (0 votes)
