Limite de una Función con Valor Absoluto en el Denominador Límites Algebraicos Límite en un Punto
Summary
TLDR本视频讲解了如何计算函数在特定点的极限,重点是对函数 f(x) = 5x / |x + 4| 在 x = -4 处的极限进行分析。通过计算左右极限,我们发现无论从右边还是左边逼近,极限都趋向于负无穷。因此,该点的极限不存在。视频通过详细的步骤和图示,帮助理解极限的计算过程,特别是如何处理绝对值函数的分母为零的情况。
Takeaways
- 😀 计算极限时,要检查左右极限是否相等,并且它们的值应该是有限的,而不是无限大的。
- 😀 本题中,我们计算的是当 x 趋近于 -4 时,函数 5x / |x + 4| 的极限。
- 😀 函数 f(x) = 5x / |x + 4| 在 x = -4 时不定义,因为在该点分母为零。
- 😀 为了验证极限是否存在,必须计算右侧和左侧的极限,并确保它们相等且是有限的。
- 😀 右侧极限(x > -4)时,|x + 4| 等于 x + 4,因此极限为 -∞。
- 😀 左侧极限(x < -4)时,|x + 4| 等于 -(x + 4),计算结果也是 -∞。
- 😀 因为右侧和左侧的极限都趋向于 -∞,所以函数在 x = -4 处的极限是 -∞。
- 😀 由于左右极限都趋向于 -∞,而不是一个有限值,函数在 x = -4 处的极限不存在。
- 😀 图形上,函数在 x = -4 附近会趋向于 -∞,不论是从右侧还是左侧。
- 😀 总结:如果左右极限相等且为有限值,函数在该点的极限才存在;否则,极限不存在。
Q & A
什么是绝对值函数?
-绝对值函数是指将一个数的负值转换为正值,例如,|x + 4| 会根据 x + 4 的符号而表现不同:当 x + 4 ≥ 0 时,|x + 4| = x + 4;当 x + 4 < 0 时,|x + 4| = -x - 4。
在本例中,为什么函数在 x = -4 处没有定义?
-函数 f(x) = 5x / |x + 4| 在 x = -4 处没有定义,因为当 x = -4 时,|x + 4| = 0,导致分母为 0,除以零是没有定义的。
什么是侧限的概念?
-侧限是指当 x 接近某个特定值时,函数从左侧(x 值比该点小)或右侧(x 值比该点大)趋近的极限值。侧限要求左侧极限和右侧极限相等且有限,才能得出该点的极限值。
如何计算右侧极限?
-右侧极限是指当 x 从比 -4 大的值趋近 -4 时的极限。在本例中,x > -4 时,|x + 4| = x + 4,因此函数成为 5x / (x + 4),计算得右侧极限是负无穷。
如何计算左侧极限?
-左侧极限是指当 x 从比 -4 小的值趋近 -4 时的极限。在本例中,x < -4 时,|x + 4| = -x - 4,因此函数成为 5x / (-x + 4),计算得左侧极限也是负无穷。
为何右侧和左侧的极限都为负无穷?
-当 x 接近 -4 时,分母趋近于零,而分子恒为负数。无论是从右侧接近还是左侧接近,结果都是负无穷。这是因为分子和分母的符号始终使得最终结果为负无穷。
什么情况下函数的极限不存在?
-当函数的左右极限不相等,或者其中一个极限是无限大的情况下,函数在该点的极限就不存在。在本例中,左右极限都为负无穷,因此极限不存在。
为什么说这个极限是无穷大的?
-这个极限是无穷大的,因为当 x 接近 -4 时,分母的绝对值接近零,而分子始终是负数,因此值会趋近于负无穷。这表明极限不存在且趋向无穷。
如何通过图形理解这个极限?
-通过图形可以看到,当 x 接近 -4 时,函数的值会快速下降到负无穷。在 -4 处,函数没有定义,因此图形在这个点有一个断点,且从左侧和右侧都趋向负无穷。
如果极限存在,会有什么样的结果?
-如果极限存在,左右极限必须相等,并且应该是一个有限的数值。如果存在且是有限的,那么可以给出一个具体的极限值。如果是无穷大或无穷小,则说明极限不存在。
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Funciones pares e impares explicación gráfica

03. Derivative using definition as limit

Límites cuando x tiende al infinito | Profe Andalón

Cálculo Integral 02:Sumas infinitas. Infinite sums.
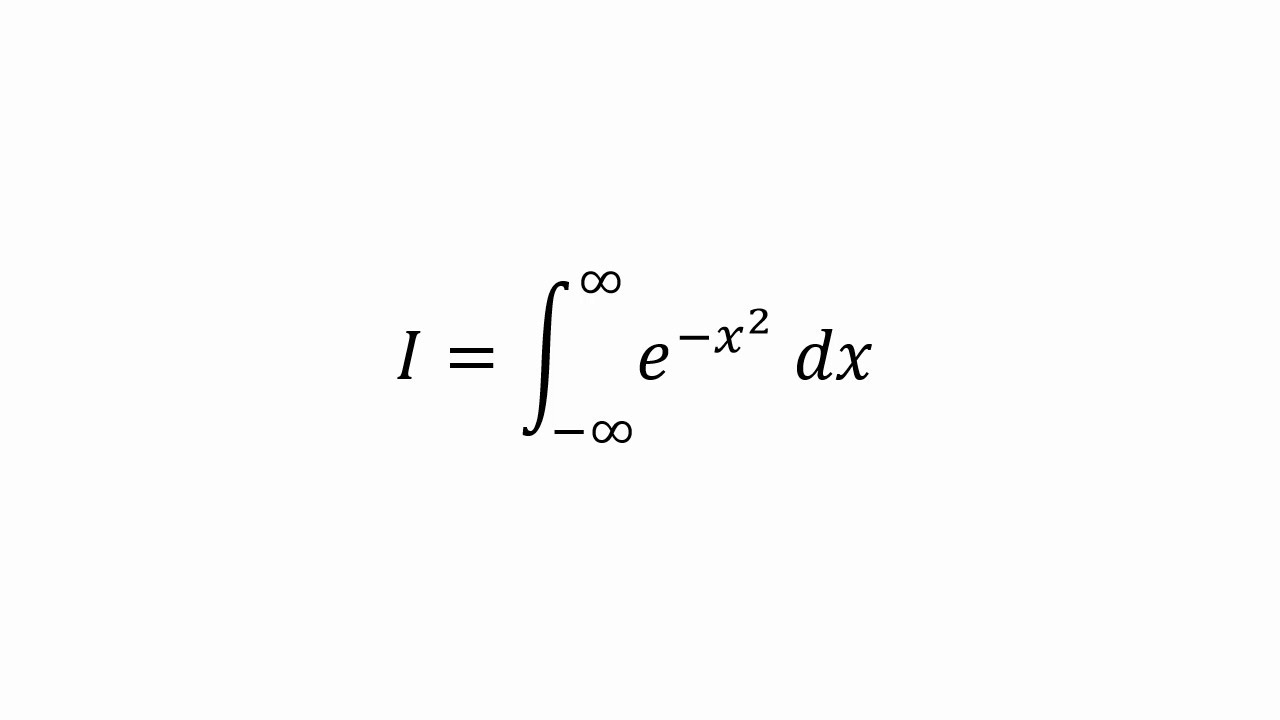
The Gaussian Integral

Teorema fundamental del cálculo: definición y ejemplos

Varberg《Calculus》微积分 Chapter 1 Limits #3 |无穷小
5.0 / 5 (0 votes)
