The Basic Mathematics of Pokemon
Summary
TLDRIn this engaging video, Bradley Swart explores the dynamics of a Pokémon card's 'Wreak Havoc' ability through a blend of anecdotal and mathematical approaches. He contrasts his son's intuitive estimate of card damage with his own calculated expectation using Monte Carlo simulations and Excel. By breaking down the probabilities involved, Swart demonstrates how to derive the expected value of card effects through various methodologies, ultimately leading to a deeper understanding of probability and infinite series. This case study not only illustrates the fun of Pokémon but also highlights the intersection of gaming and mathematics.
Takeaways
- 😀 Pokémon has been a cultural phenomenon for over 20 years, with renewed interest driven by children.
- 😀 The speaker explores the expected value of a Pokémon card's effect through both intuition and mathematics.
- 😀 A specific Pokémon card, Guilleridos, has an attack that involves flipping a coin repeatedly until tails, impacting the opponent's deck.
- 😀 The speaker engages their child in estimating how many cards might be affected by this attack, revealing differences in intuition.
- 😀 A Monte Carlo simulation is used to approximate the average number of cards discarded, showing that the expected value is around two.
- 😀 The simulation highlights the independence of coin flips and how probabilities affect outcomes in games.
- 😀 The speaker discusses transitioning from simulation to more analytical approaches, including using Excel for calculations.
- 😀 An infinite series is introduced to mathematically prove the expected value, resulting in a deeper understanding of probability.
- 😀 The mathematical proof includes summation techniques, illustrating how the series converges to the expected value.
- 😀 The video concludes with a reflection on different methodologies for solving a seemingly simple problem, emphasizing the richness of mathematical exploration.
Q & A
What is the main subject of the video?
-The video discusses the Pokémon card 'Guilleridos' and its ability 'Wreak Havoc,' examining both the expectations of a child regarding its effectiveness and the underlying mathematics.
How does the 'Wreak Havoc' ability work?
-'Wreak Havoc' allows the player to flip a coin repeatedly until they land on tails, discarding two cards from the opponent's deck for each heads flipped before getting tails.
What did Bradley Swart's son estimate the average number of cards discarded would be?
-Swart's son estimated that about four cards would be discarded.
What was Swart's own calculation regarding the average number of cards discarded?
-Swart calculated that, on average, about two cards would be discarded.
What method did Swart use to simulate the coin flips?
-He used a Monte Carlo simulation implemented in Python to flip a coin a million times and estimate the expected value.
What mathematical concept does Swart introduce to analyze the card's effect?
-Swart introduces the concept of an infinite series to mathematically analyze the expected outcomes of the card's ability.
How does Swart demonstrate the probability distribution of the card's effect?
-He discusses a flowchart representing the probabilities of flipping heads or tails and how many cards can be discarded based on those flips.
What was the outcome of the simulation regarding the number of cards discarded?
-The simulation confirmed that the average number of cards discarded per use of 'Wreak Havoc' was around two, aligning with Swart's mathematical expectations.
What educational purpose does the video serve?
-The video aims to bridge gaming and mathematics, showing how different analytical methods can be used to understand game mechanics more deeply.
What is the significance of the infinite series in this context?
-The infinite series helps provide a mathematical proof of the expected value of cards discarded, demonstrating how complex mathematical concepts can be applied to simple game mechanics.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

How Your Low Self Esteem Impacts Your Relationships

Invasive Species: Ships Are Fighting Back!

Вбивчий вплив стресу. Фільм Роберта Сапольскі
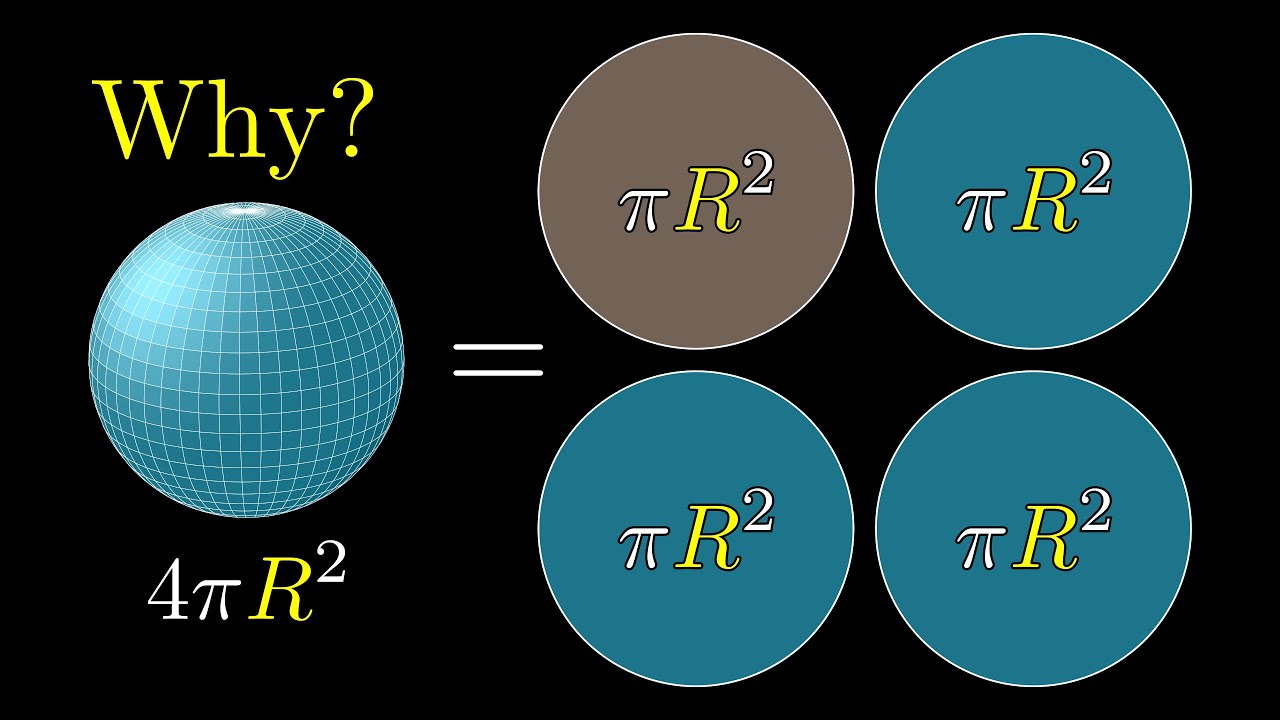
But why is a sphere's surface area four times its shadow?

Pokemon Timeline Explained | Legendary and Mythical Pokemon

Cambridge Mathematician Reacts to Animation vs Geometry
5.0 / 5 (0 votes)
