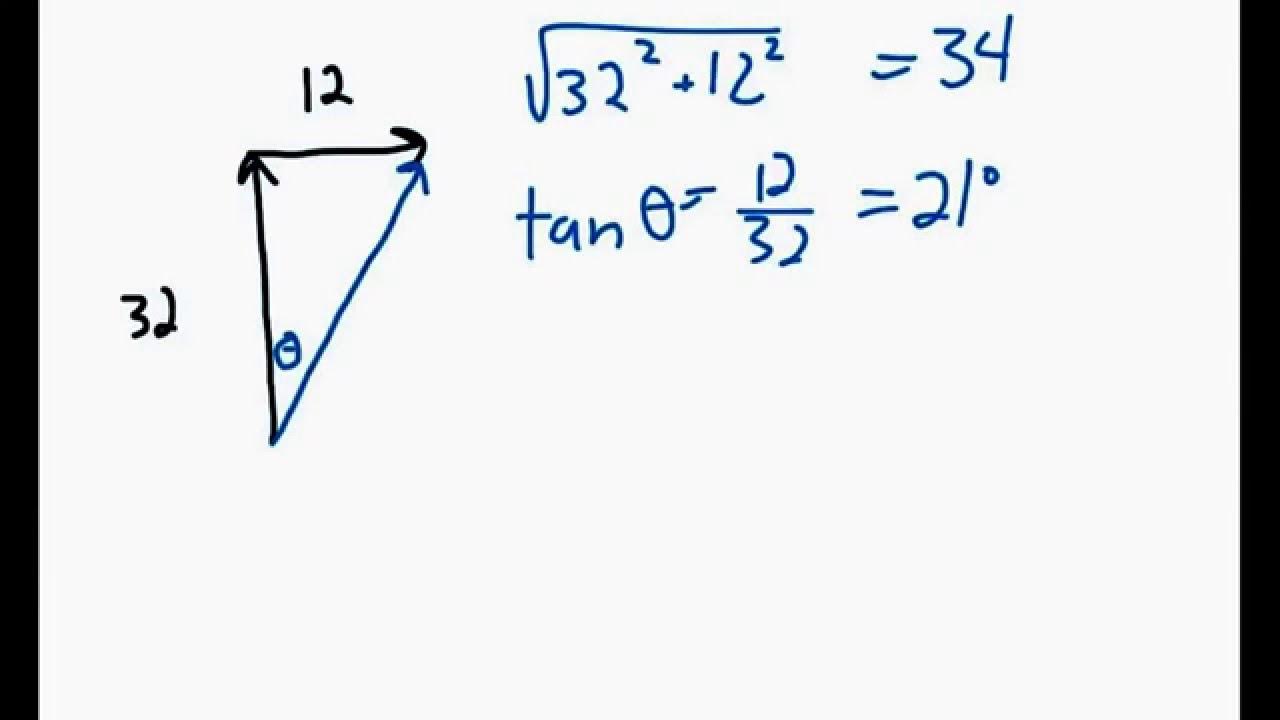Vector Resolution
Summary
TLDRThis video tutorial covers vector resolution, explaining how to determine the components of a vector using both graphical and trigonometric methods. It demonstrates the process of projecting a vector onto the X and Y axes and using sine, cosine, and tangent functions to calculate the components of a vector. The tutorial also walks through practical examples using real-world measurements, offering useful tips and shortcuts for calculations. Viewers are encouraged to apply their knowledge using additional resources available on the website and apps for further practice and review.
Takeaways
- 🔍 Vector resolution involves breaking down a vector into its X and Y components.
- 📏 The graphical method uses perpendicular projections from the vector onto the X and Y axes to find the vector components.
- 🖊️ To determine vector components graphically, you draw perpendicular lines from the arrowhead to the axes and measure the lengths of these components.
- 📐 The trigonometric method involves using sine, cosine, and tangent functions to calculate the vector components based on the vector's angle and magnitude.
- 📊 The sine function is used to calculate the Y component (opposite side), and the cosine function is used to calculate the X component (adjacent side) of the vector.
- 📚 To use the trigonometric method, you must know the magnitude of the vector and the angle it makes with a reference direction, typically counterclockwise from east.
- 🧮 The equations AX = A * cos(θ) and AY = A * sin(θ) are shortcuts for calculating vector components when the angle is measured counterclockwise from east.
- 🌍 The graphical method requires drawing vectors to scale, while the trigonometric method involves direct calculation with trigonometric ratios.
- 📝 A positive result for the X component (cosine) means the vector points east, while a negative result indicates west. For the Y component (sine), positive means north, and negative means south.
- 🎯 Practice with real-world examples and try resources such as 'Calculator Pad' questions and the 'Minds on Physics' app to reinforce your understanding of vector resolution.
Q & A
What is vector resolution?
-Vector resolution is the process of determining the magnitude and direction of a vector's components, which are the projections of the vector along the X and Y axes.
How does the graphical method of vector resolution work?
-The graphical method involves drawing perpendicular projections from the vector's arrowhead to the X and Y axes, then measuring the lengths of these projections to determine the magnitudes of the components.
How can you use a scale when applying the graphical method?
-To use a scale, you first draw the vector to scale, then measure the lengths of the vector components, and finally convert those lengths into real-world magnitude values using the defined scale.
What role do trigonometric functions play in vector resolution?
-Trigonometric functions (sine, cosine, and tangent) relate the sides of a right triangle to its angles and are used to calculate the X and Y components of a vector based on the vector’s angle and magnitude.
How do you determine the X and Y components of a vector using the trigonometric method?
-You use the cosine of the angle to calculate the X component (adjacent side) and the sine of the angle to calculate the Y component (opposite side), both multiplied by the vector’s magnitude.
What is the advantage of using the 'counterclockwise from east' convention for angles?
-The 'counterclockwise from east' convention simplifies the use of shortcut equations for vector resolution, such as using cos(θ) for the X component and sin(θ) for the Y component.
What do positive and negative signs indicate when using the shortcut equations?
-For the X component, a positive sign indicates the direction is east, and a negative sign means west. For the Y component, a positive sign means north, and a negative sign means south.
Why is it important to correctly identify the angle in vector resolution?
-Identifying the correct angle ensures accurate use of the trigonometric functions to find the vector components. Using an incorrect angle could lead to incorrect results for the components.
What resources are available for further practice with vector resolution?
-The video recommends trying exercises on the 'Calculator Pad' at the physics classroom website, using the 'Minds on Physics' app (Module DP5), or reading tutorials available on the website.
What is the importance of understanding vector components in physics?
-Understanding vector components is crucial for analyzing forces, motion, and other physical quantities in different directions, which is a fundamental aspect of solving problems in physics.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
5.0 / 5 (0 votes)