Math 251 - What is a limit?
Summary
TLDRIn this Math 251 lesson, the concept of limits in calculus is introduced. The instructor breaks down the formal definition, explaining how a function's values approach a certain real number 'l' as the input 'x' approaches a specific value 'a'. Using both graphical and tabular examples, the lesson illustrates how to determine limits, even when the function is undefined at 'x=a', emphasizing the importance of the function's behavior around 'a' rather than at the point itself.
Takeaways
- 📘 The concept of a limit in calculus is introduced, focusing on how function values approach a certain number.
- 📐 A function f(x) must be defined on an interval containing a point 'a', except possibly at 'a' itself.
- 🔢 The limit 'l' is a real number that represents the y-value the function approaches as x approaches 'a'.
- 📉 As x values get closer to 'a', the corresponding f(x) values should get closer to 'l'.
- 📊 The limit is symbolized as 'lim (x→a) f(x) = l', indicating f(x) approaches l as x approaches a.
- 📈 An example is given with a quadratic graph to illustrate how to find the limit as x approaches a specific value.
- 📋 Even with a table of values, the concept of a limit can be applied to determine what the function values approach.
- 🚫 The function does not need to be defined at the point 'a'; it's acceptable to have a 'hole' at that point.
- 📌 The limit exists and is valid even if the function is undefined at the point where x is approaching.
- 👋 The video concludes with a reminder that there are more lessons to follow on this topic.
Q & A
What is the primary focus of the lesson in the transcript?
-The lesson focuses on explaining the concept of limits in calculus, specifically what it means for the limit of a function f(x) to approach a value l as x approaches a certain point a.
How is the definition of a limit presented in the lesson?
-The definition of a limit is presented as a function f(x) being defined at all points in an open interval containing a, except possibly at a itself, with the function values approaching a real number l as x values approach a.
What does it mean for a function to be defined at all values in an open interval containing a?
-It means the function is defined throughout the interval except possibly at the point a, allowing for a 'hole' at that point without affecting the limit.
Why is it okay for the function to have a hole at point a?
-Having a hole at point a is acceptable because the definition of a limit only requires the function to be defined in an interval around a, not necessarily at a itself.
What is the symbolic representation of a limit as x approaches a?
-The symbolic representation of a limit as x approaches a is written as 'lim (x→a) f(x) = l', indicating that f(x) approaches l as x approaches a.
How does the lesson use a graph to illustrate the concept of a limit?
-The lesson uses a graph to show that as x values get closer to a, the corresponding y values (f(x)) get closer to a specific real number l, which is the limit.
What is an example of finding a limit using a graph provided in the lesson?
-An example is finding the limit as x approaches 6 on a quadratic graph, where it's observed that as x values approach 6 from both sides, the y values approach 2.
How can you determine a limit when given a table of values instead of a graph?
-With a table, you look at how the y values (f(x)) change as the x values approach the point of interest from both sides to see if they consistently approach a certain value l.
What does it mean if the function is undefined at the point x equals a?
-If the function is undefined at x equals a, it means there is a hole or a discontinuity at that point, but it does not prevent the existence of a limit as x approaches a.
What is the significance of the y value in the context of limits?
-The y value is significant because it represents the value that the function f(x) approaches as x approaches a certain point a, which is the essence of the limit concept.
How does the lesson emphasize the importance of approaching a from both sides when considering limits?
-The lesson emphasizes that to find a limit, one must consider how the function values behave as x approaches a from both directions, ensuring the function's behavior is consistent.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة

Calculus (Version #2) - 1.1 Limits Graphically

Introduction to limits 2 | Limits | Precalculus | Khan Academy

Calculus Made EASY! Learning Calculus
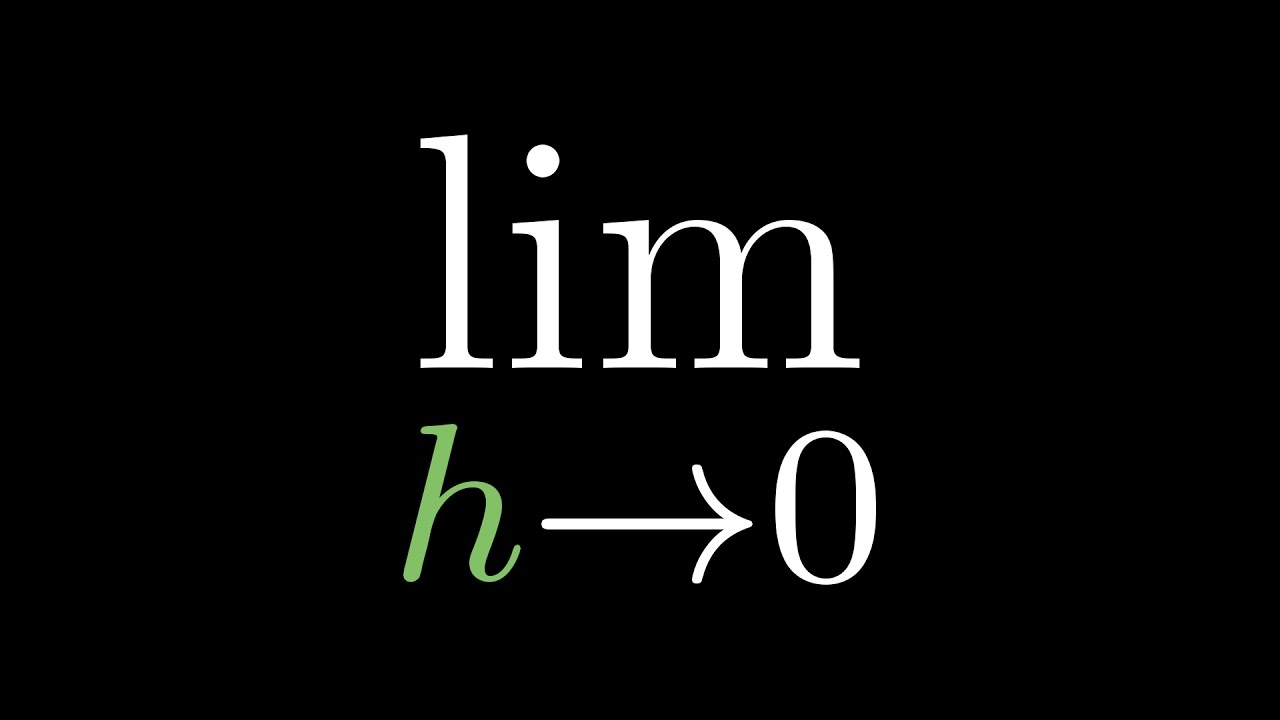
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

04. Limites e Continuidade. | Cálculo I.

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)
5.0 / 5 (0 votes)
