Sumas de Riemann - Ej.1 (Paso a paso | Cuadrática)
Summary
TLDREl video ofrece una explicación detallada sobre cómo resolver una integral definida utilizando el método de la suma de Riemann. A través de un enfoque paso a paso, el presentador guía al espectador para identificar valores clave como 'b' y 'fx', calcular el intervalo 'Δx' y aplicar la fórmula de la suma de Riemann. Se desglosan los cálculos para simplificar el integrando y se aplica la sumatoria, culminando con la toma del límite cuando 'n' tiende al infinito para obtener el resultado final. El video es una herramienta educativa para comprender mejor los conceptos de cálculo integral.
Takeaways
- 📚 El vídeo trata sobre cómo resolver una integral definida utilizando el método de la suma de Riemann.
- 🔍 Se explica que el método de la suma de Riemann puede parecer complicado, pero se desglosa en pasos claros para su comprensión.
- 📐 Se identifican los valores de 'a', 'b' y la función 'f(x)' como los primeros pasos para resolver la integral.
- 📝 Se menciona la importancia de comparar los valores de 'b' y 'f(x)' con los límites de la integral.
- ✏️ Se detalla el proceso de cálculo del intervalo 'Δx' y cómo sustituir estos valores en la fórmula.
- 📉 Se explica cómo calcular 'xᵢ' y 'f(xᵢ)', que son partes fundamentales de la fórmula de la suma de Riemann.
- 🔢 Se aborda la manipulación algebraica de las expresiones para simplificar la fórmula y facilitar los cálculos.
- 🧮 Se resalta la necesidad de aplicar propiedades de productos notables y el uso de potencias para simplificar la expresión.
- 🔄 Se describe el proceso de multiplicar el resultado de 'f(xᵢ)' por 'Δx' para obtener la suma parcial.
- 🌐 Se menciona la aplicación de la sumatoria para combinar todos los términos y obtener una expresión más compacta.
- 📉 Se explica cómo aplicar las fórmulas de sumatoria y simplificar la expresión obtenida.
- 📖 Se enfatiza la importancia de tomar el límite cuando 'n' tiende al infinito para obtener el resultado final de la integral.
Q & A
¿Qué método se utiliza para resolver la integral definida en el guion?
-Se utiliza el método de la suma de Riemann para resolver la integral definida.
¿Cuál es el primer paso al resolver la integral con el método de Riemann?
-El primer paso es identificar el valor de 'b' y el valor de 'fx' a partir de la integral proporcionada.
¿Cómo se determina el intervalo 'Δx' en el método de Riemann?
-El intervalo 'Δx' se determina como la diferencia entre 'b' y 'a', donde 'a' es el límite inferior y 'b' es el límite superior de la integral.
¿Qué es 'xᵢ' en el contexto del método de Riemann?
-'xᵢ' representa el punto de evaluación dentro del intervalo dividido, generalmente es el punto medio o el punto de corte del intervalo 'Δx'.
¿Cómo se calcula 'f(xᵢ)' en el método de Riemann?
-'f(xᵢ)' se calcula sustituyendo 'xᵢ' en la función 'f(x)' que está siendo integrada.
¿Qué significa 'n' en el método de Riemann?
-'n' representa el número de subintervalos en los que se divide el intervalo total, y se utiliza para calcular 'Δx' como '(b-a)/n'.
¿Cuál es la fórmula para el área aproximada bajo la curva usando el método de Riemann?
-La fórmula para el área aproximada es la suma de los productos de 'f(xᵢ)' y 'Δx', donde 'f(xᵢ)' es la función evaluada en cada punto 'xᵢ'.
¿Cómo se aplica la propiedad de los productos notables en el cálculo de 'f(xᵢ)'?
-Los productos notables se aplican al expandir y simplificar la expresión de 'f(xᵢ)' cuando se sustituye 'xᵢ' en la función 'f(x)'.
¿Qué es la sumatoria y cómo se usa en el método de Riemann?
-La sumatoria es una notación matemática para la suma de un conjunto de términos. En el método de Riemann, se usa para sumar el área de todos los rectángulos o trapecios que se utilizan para aproximar la integral.
¿Cómo se calcula el límite cuando 'n' tiende al infinito en el método de Riemann?
-El límite cuando 'n' tiende al infinito se calcula sustituyendo 'n' por un infinito en la sumatoria y simplificando el resultado para obtener el valor exacto de la integral.
Outlines

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنMindmap

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنKeywords

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنHighlights

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنTranscripts

هذا القسم متوفر فقط للمشتركين. يرجى الترقية للوصول إلى هذه الميزة.
قم بالترقية الآنتصفح المزيد من مقاطع الفيديو ذات الصلة
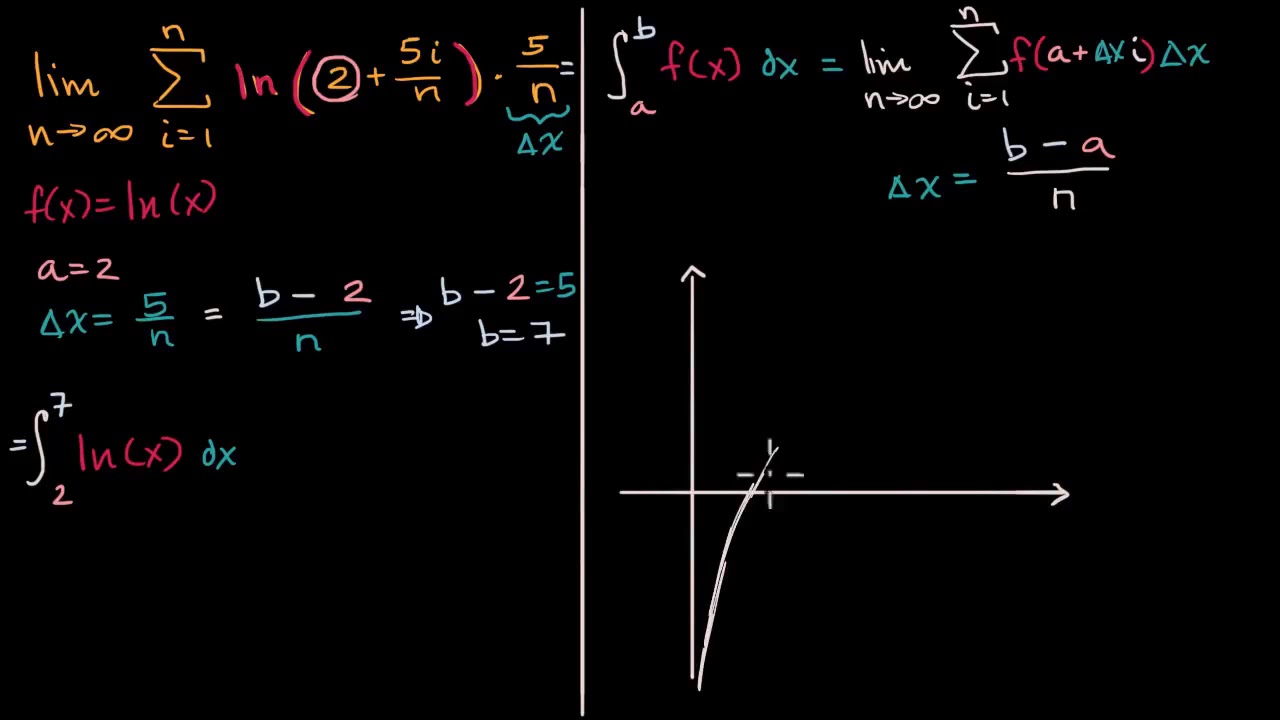
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Suma de Riemann, paso a paso, MUY FÁCIL

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español

Integral de Seno | Integrales por Sustitución - Cambio de variable | Ejemplo 18

Integración por fracciones parciales | Ejemplo 2 División

Solución de problemas con Sistemas de Ecuaciones Lineales 2x2 | Ejemplo 8
5.0 / 5 (0 votes)
