Section 6.2 - Trig integrals and substitution - Part 1

Summary

This educational video script focuses on techniques for calculating integrals involving trigonometric functions, specifically trig integrals. It introduces three types of substitutions useful for simplifying complex integrals, emphasizing the memorization of key trigonometric identities and their derivatives. The script illustrates step-by-step strategies for integrating powers of sine and cosine, using examples to demonstrate how to handle both odd and even powers. It also covers half-angle formulas and their application in integration, providing a comprehensive guide to tackling advanced trigonometric integrals.

Takeaways

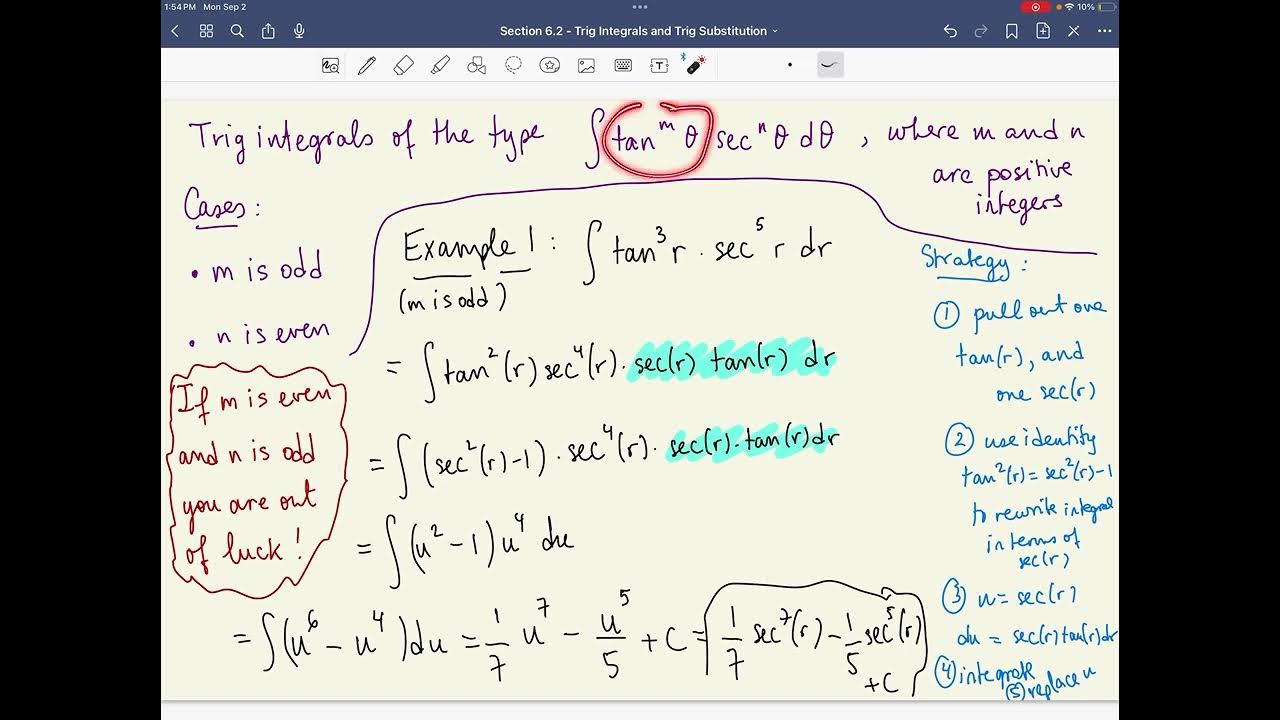
• 📚 The section focuses on calculating integrals involving trigonometric functions, specifically integrals with powers of sine, cosine, tangent, secant, and their combinations.
• 🔄 Three different kinds of substitutions are introduced to simplify the integration process, which are variations of the standard u-substitution.
• 📐 Trigonometric identities are essential for these calculations, and the script emphasizes memorizing these for successful integration.
• 👉 The identity sin²θ + cos²θ = 1 is derived from the Pythagorean theorem applied to a unit circle, and it's crucial for simplifying expressions.
• 🧩 Half-angle formulas are introduced to express sin²θ and cos²θ in terms of cosine of double angles, which are useful for integration.
• 📉 The derivatives of trigonometric functions like sine, cosine, tangent, secant, and their reciprocals are reviewed as they are needed for integration by parts.
• 🔢 The strategy for integrating powers of sine and cosine involves separating out one power and rewriting the rest using trigonometric identities, especially when the powers are odd.
• 🔄 When both powers in the integral are even, the strategy involves using half-angle identities to rewrite the integral in terms of cosine squared, which can then be integrated.
• 📝 Examples are provided to illustrate the strategies for different cases, including when the power of sine is odd, the power of cosine is odd, and when both powers are even.
• 🔍 The script concludes with a more complex example that demonstrates the application of the discussed strategies and identities for integrating more challenging trigonometric expressions.

Q & A

What are trig integrals?

Trig integrals are integrals that involve powers of sine and cosine, as well as integrals that involve powers of tangent, secant, and other related trigonometric functions.

What are the three different kinds of substitutions mentioned in the script for simplifying integrals?

The script does not explicitly name the three different kinds of substitutions, but it implies that they are methods used to simplify integrals involving trigonometric functions, particularly those that might be difficult to compute directly.

Why are trigonometric identities important in calculating certain integrals?

Trigonometric identities are important because they allow us to rewrite expressions in forms that are easier to integrate, often by simplifying the powers of trigonometric functions or transforming them into more manageable expressions.

What does the notation sin^2(θ) represent?

The notation sin^2(θ) represents the square of the sine function of θ, meaning sine of θ is taken and then squared.

What is the significance of the identity sin^2(θ) + cos^2(θ) = 1?

The identity sin^2(θ) + cos^2(θ) = 1 is significant because it represents the Pythagorean theorem in the context of the unit circle, where the square of the x-coordinate (cosine of θ) plus the square of the y-coordinate (sine of θ) equals the square of the radius (which is 1 for the unit circle).

What are half-angle formulas and why are they useful for integration?

Half-angle formulas are trigonometric identities that express the sine and cosine of half an angle in terms of the sine and cosine of the full angle. They are useful for integration because they allow us to express powers of sine and cosine in a form that can be more easily integrated.

What is the difference between secant and the inverse cosine function?

Secant is defined as 1/cos(θ), which is the reciprocal of the cosine function. The inverse cosine function, denoted as cos^(-1)(θ) or cos^(-1)(x), is a function that gives the angle whose cosine is a given value, and it is not the reciprocal of the cosine function.

How does the identity tan(θ) + 1 = sec^2(θ) help in integration?

The identity tan(θ) + 1 = sec^2(θ) is helpful in integration because it allows us to express the sum of the tangent function and 1 as the square of the secant function, which can then be integrated more easily using standard integral formulas.

What strategy is used when the power of sine is odd in a trig integral?

When the power of sine is odd in a trig integral, the strategy is to separate out one sine term and rewrite the remaining power of sine using the identity sin^2(θ) = 1 - cos^2(θ), then use a substitution with u = cos(θ) to simplify the integral.

How do you handle integrals where both the powers of sine and cosine are even?

For integrals where both the powers of sine and cosine are even, the strategy involves using trigonometric identities to rewrite the expression in terms of cosine squared and then applying half-angle identities to simplify the integral.