Maths Olympiad Question | A nice algebraic equation | You should know this trick!
Summary
TLDRThe video script presents a mathematical problem involving the evaluation of an expression with x raised to the fourth power. The presenter uses substitution by setting U = 1 - x and applies the binomial theorem to simplify and solve for x. After finding the value of U, they determine x has four possible solutions, showcasing the process with clear explanations and engaging the audience to follow along.
Takeaways
- 📚 The video discusses solving the equation \(x^4 + (2 - x)^4 = 34\) to find the value of x.
- ✏️ The approach begins by substituting \(U = 1 - x\), leading to transformations for both x and \(2 - x\).
- 🔄 Substituting these transformations into the original equation results in a binomial expansion using the binomial theorem.
- 🧮 The binomial expansion is detailed, using coefficients from the binomial theorem to expand \( (1 - U)^4 \) and \( (1 + U)^4 \).
- ➗ After expanding, terms are combined and simplified, leading to an equation in terms of U, which is then solved using factorization.
- 🧩 The factorized equation yields two quadratic equations, \( U^2 + 8 = 0 \) and \( U^2 - 2 = 0 \), each solved separately.
- ⚙️ The solutions for U are complex numbers for the first equation and real numbers for the second.
- 🔍 Substituting the values of U back into the expression \(x = 1 + U\), gives four possible solutions for x.
- 🧑🏫 The final solutions for x are \(x_1 = 1 + 2\sqrt{2}i\), \(x_2 = 1 - 2\sqrt{2}i\), \(x_3 = 1 + \sqrt{2}\), and \(x_4 = 1 - \sqrt{2}\).
- 👍 The video concludes by summarizing the four solutions, reminding viewers to follow and subscribe for more content.
Q & A
What is the first step taken to evaluate the equation x^4 + 2 - x^4 = 34?
-The first step is to substitute u = 1 - x, allowing the equation to be simplified by replacing expressions involving x with u.
How is the value of 2 - x derived after substituting u = 1 - x?
-After substituting u = 1 - x, the value of 2 - x is simplified to 1 + u.
Why is the binomial theorem used in this problem?
-The binomial theorem is used to expand the expressions (1 - u)^4 and (1 + u)^4, which are crucial for simplifying and solving the equation.
What is the significance of the expansion of (1 - u)^4 and (1 + u)^4?
-The expansion helps to identify and simplify terms, leading to a final equation that can be solved for u, and subsequently for x.
How are the terms of the binomial expansion combined to simplify the equation?
-The like terms from the expansions of (1 - u)^4 and (1 + u)^4 are added together, which allows for the elimination of certain terms and further simplification of the equation.
What does the equation simplify to after factoring and canceling out common terms?
-After factoring and canceling out common terms, the equation simplifies to u^4 + 6u^2 - 16 = 0.
How is the quadratic equation u^4 + 6u^2 - 16 = 0 solved?
-The equation is solved by grouping and factorization, leading to two possible quadratic equations u^2 + 8 = 0 and u^2 - 2 = 0.
What are the possible values of u derived from the quadratic equations?
-The possible values of u are u = ±2√2i from u^2 + 8 = 0 and u = ±√2 from u^2 - 2 = 0.
How are the values of x determined from the values of u?
-The values of x are determined by substituting the values of u back into the equation x = 1 - u, resulting in four possible solutions for x.
What are the final four solutions for x?
-The final four solutions for x are x1 = 1 + 2√2i, x2 = 1 - 2√2i, x3 = 1 + √2, and x4 = 1 - √2.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Jika lim x->-3 (x^2+4x+3)/(x+3)=a-1,nilai a adalah...

Menentukan Salah Satu Fungsi Jika Diketahui Fungsi Komposisinya

Evaluating Functions - Basic Introduction | Algebra

Solving Quadratic Equations Using Factoring and Extracting the Square Roots (Module 1 Part 2)

Value of cos pi || cos π value || cos π || cos pi
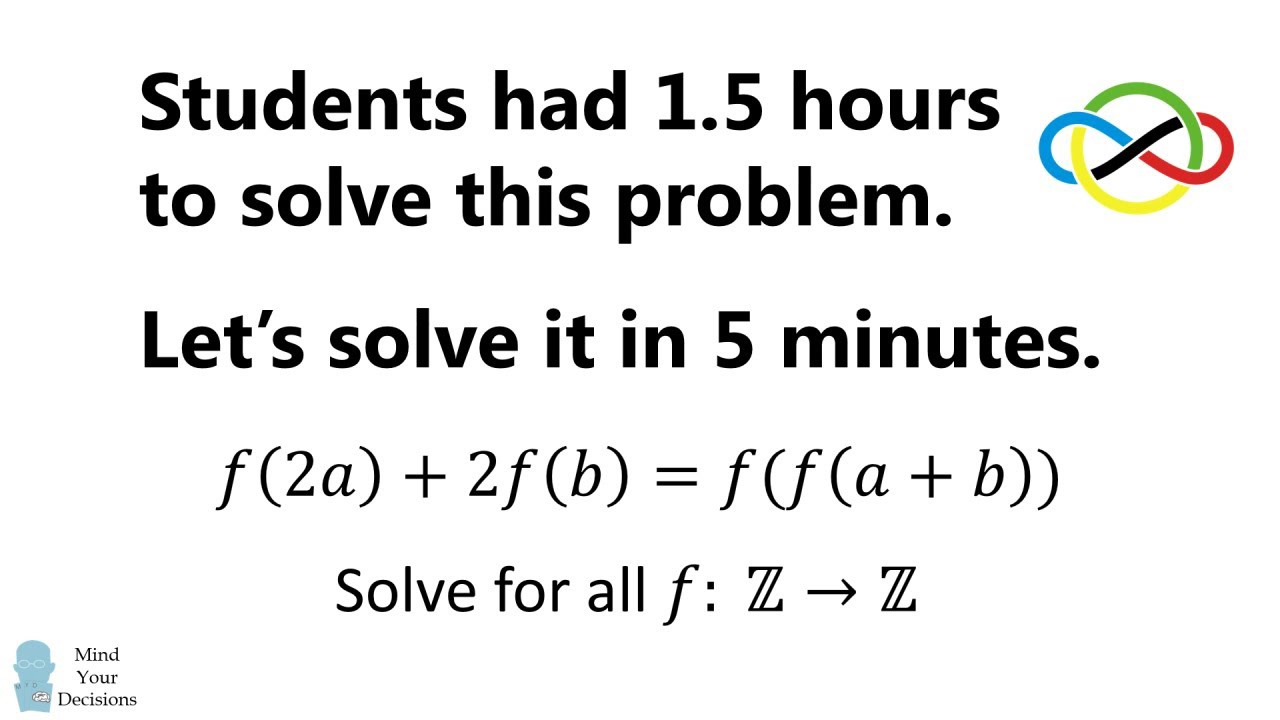
Solving An Insanely Hard Problem For High School Students
5.0 / 5 (0 votes)
