Norway Math Olympiad Question | You should be able to solve this!
Summary
TLDRIn this educational video, the presenter demonstrates a method to solve the expression 2 to the power of 18 minus 1. They start by splitting the expression using the power of a product rule, then apply the identity (a+b)(a-b) = a^2 - b^2. After substituting 2 to the power of 9 with 512, they simplify the expression to 513 * 511 using the FOIL method. The final calculation results in 2,626,143, showcasing a clear step-by-step process that is both informative and engaging.
Takeaways
- 🔢 The problem presented is to solve \(2^{18} - 1\).
- 📝 The solution involves splitting the expression into \(2^{9} \times 2^9 - 1\).
- 🧩 The script uses the identity \(a^n \times a^m = a^{n+m}\) to simplify the expression.
- 🔑 It then applies the formula \((a + b)(a - b) = a^2 - b^2\) to further simplify the problem.
- 📈 The base \(2^9\) is calculated to be 512, which is substituted into the formula.
- 📝 The expression is then broken down into \((512 + 1) \times (512 - 1)\).
- 🔍 The numbers 513 and 511 are derived from adding and subtracting 1 from 512, respectively.
- 📚 The script uses the FOIL method (First, Outer, Inner, Last) to expand the expression.
- 📈 The multiplication is carried out with the numbers broken down into 500 + 13 and 500 + 11.
- 📊 The final calculation involves multiplying and adding the terms to get the result.
- 🎉 The final answer given is \(2^{18} - 1 = 262,143\).
Q & A
What is the mathematical expression being solved in the video?
-The mathematical expression being solved is \(2^{18} - 1\).
How does the video split the expression \(2^{18} - 1\)?
-The video splits the expression as \(2^{9} imes 2^9 - 1\), recognizing that \(2^9 imes 2\) equals \(2^{18}\).
What mathematical identity is used to simplify the expression?
-The identity \(a^n imes a^m = a^{n+m}\) is used to simplify the expression.
What is the form of the identity used in the video?
-The identity used is in the form \(a^2 - b^2 = (a+b)(a-b)\).
What is the value of \(2^9\) according to the video?
-The value of \(2^9\) is given as 512.
How is the expression \(512 + 1\) simplified in the video?
-The expression \(512 + 1\) is simplified to 513.
What is the expression for \(512 - 1\) in the video?
-The expression \(512 - 1\) is simplified to 511.
What method is used to multiply the terms in the video?
-The FOIL (First, Outer, Inner, Last) method is used to multiply the terms.
How is the multiplication of the terms broken down in the video?
-The multiplication is broken down into \(500 imes 500\), \(500 imes 11\), \(500 imes 13\), and \(13 imes 11\).
What is the final answer given for \(2^{18} - 1\) in the video?
-The final answer given is 2,626,214.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Operations with polynomials — Basic example | Math | SAT | Khan Academy
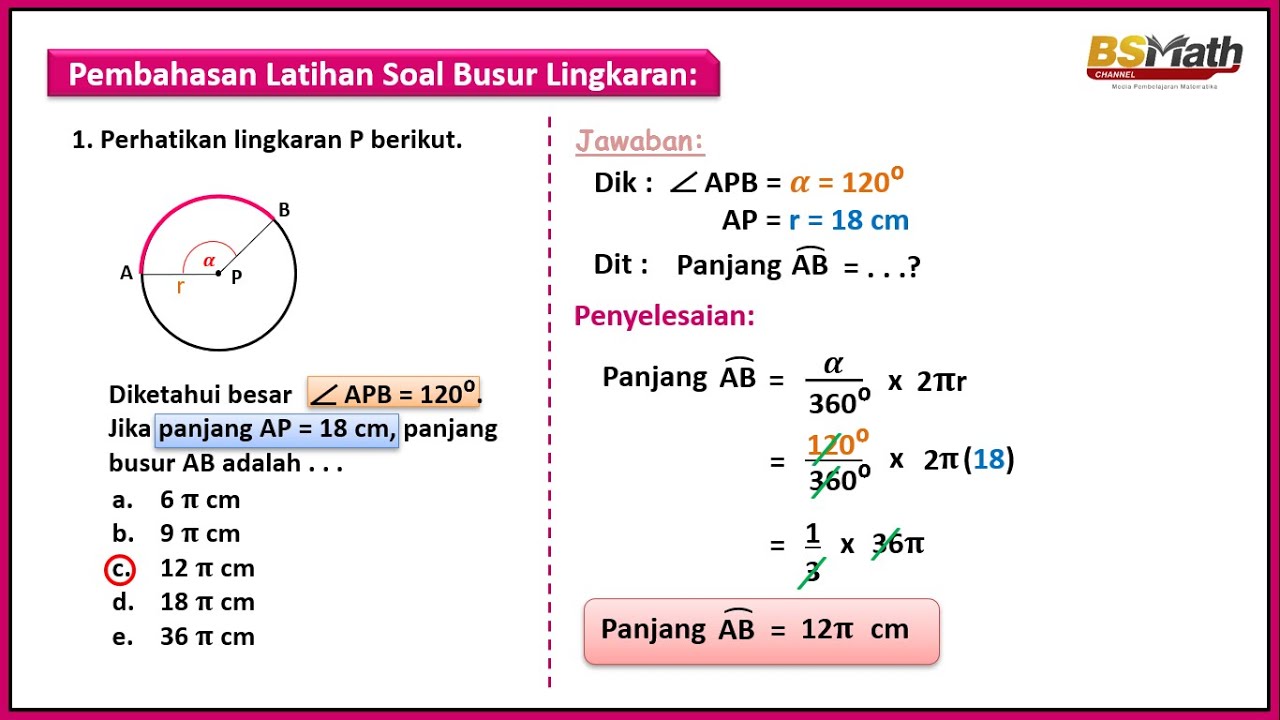
Pembahasan Latihan Soal Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka

Eric's Calculus Lecture: Evaluate the Indefinite Integral ∫e^(3x+1)dx
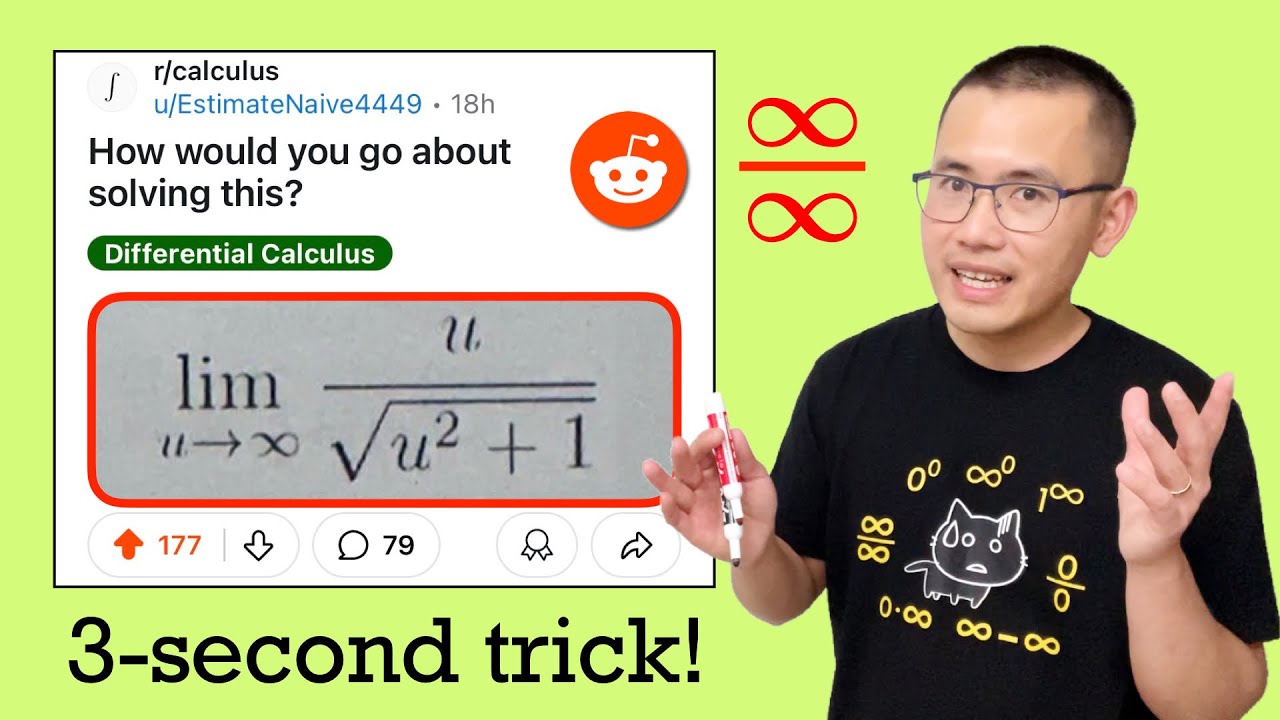
How would you go about solving this? Limit of x/sqrt(x^2+1) as x goes to infinity. Reddit inf/inf

DILATASI (PERKALIAN) || TRANSFORMASI GEOMETRI
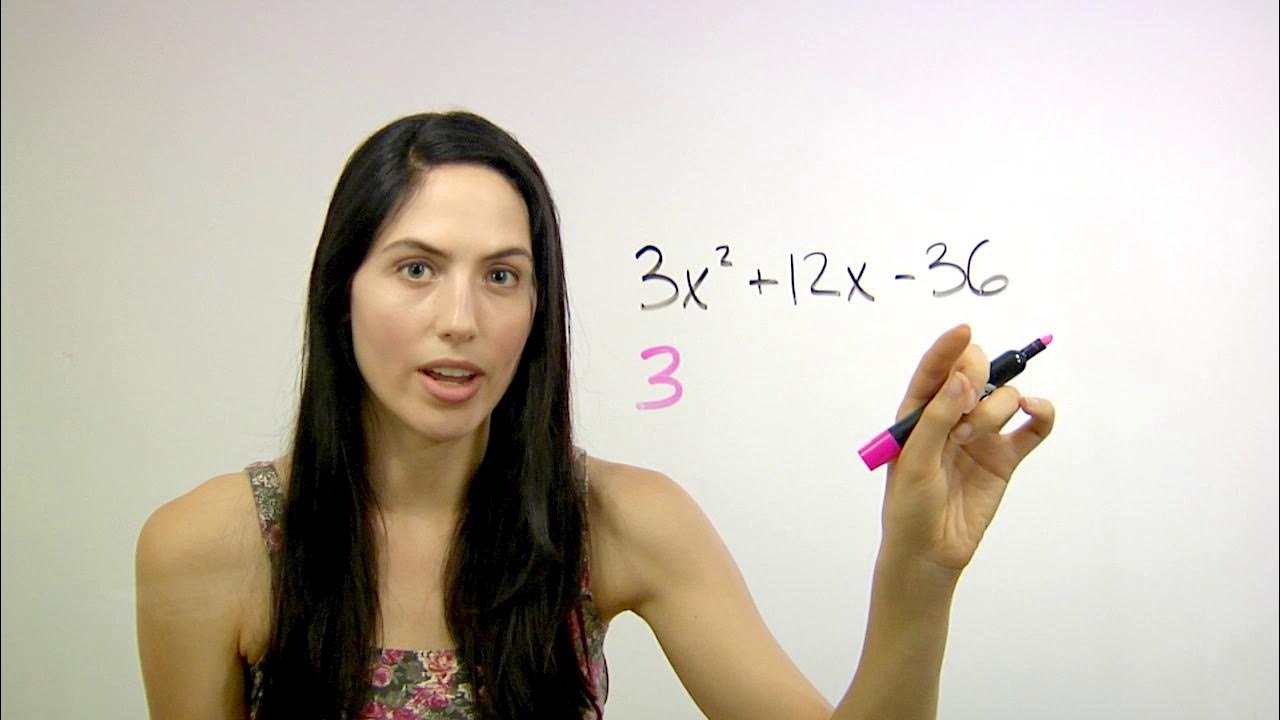
Factoring Quadratics... How? (NancyPi)
5.0 / 5 (0 votes)
