How Buildings Stand Strong: The Essential Guide to Beams & Loads

Structural Engineer Calcs

12 Dec 202307:00

Summary

TLDREn este video, exploramos el fascinante mundo de la ingeniería estructural, enfocándonos en dos vigas, B1 y B2, y cómo soportan cargas en un edificio. A través de cálculos matemáticos, se determina cuánto peso puede soportar cada viga, teniendo en cuenta cargas distribuidas de manera uniforme y triangular. También se analizan fuerzas de corte y momentos de flexión, explicando conceptos técnicos de forma sencilla. Al final, se destaca cómo la ingeniería no solo se trata de números, sino de resolver problemas del mundo real y crear espacios seguros.

Takeaways

😀 Comprender cómo los edificios se mantienen en pie es clave en la ingeniería estructural.
😀 Los elementos principales en el video son dos vigas: B1 y B2, y cómo soportan cargas.
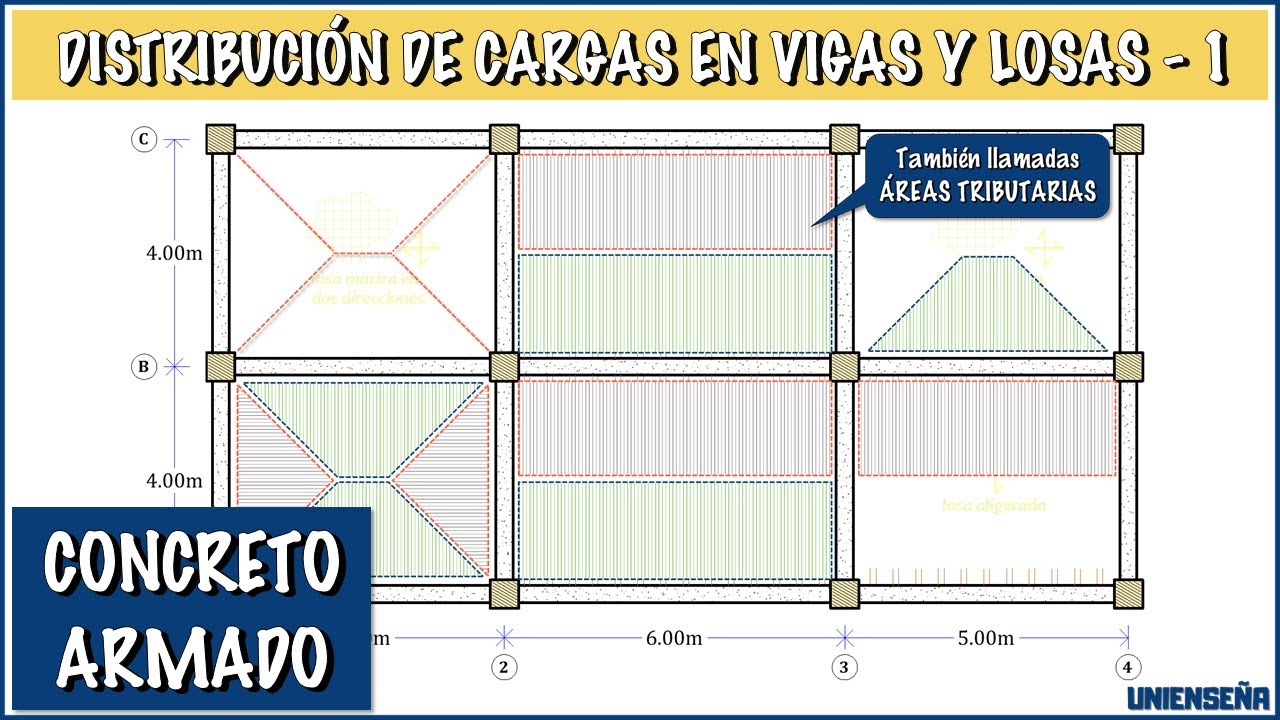
😀 La carga distribuida uniformemente y la carga triangular son dos tipos de cargas que afectan a las vigas.
😀 El cálculo para determinar cuánta carga puede soportar la viga B1 incluye tanto la carga muerta como la carga viva.
😀 La carga triangular en B1 se calcula usando un área de 16 metros cuadrados, lo que resulta en 36.8 kN de carga soportada.
😀 La carga rectangular en B1, con un área de 12 metros cuadrados, permite que la viga soporte 60.8 kN.
😀 El total de carga que la viga B1 puede soportar es de 477.6 kN, lo que demuestra su resistencia.
😀 La viga B2 soporta una carga en forma de trapecio, que tiene un área de 24 metros cuadrados y puede resistir hasta 475.0 kN.
😀 La viga B2 también recibe carga de la viga B1, llamada reacción final, sumando otros 238.8 kN, lo que lleva su total a 713.8 kN.
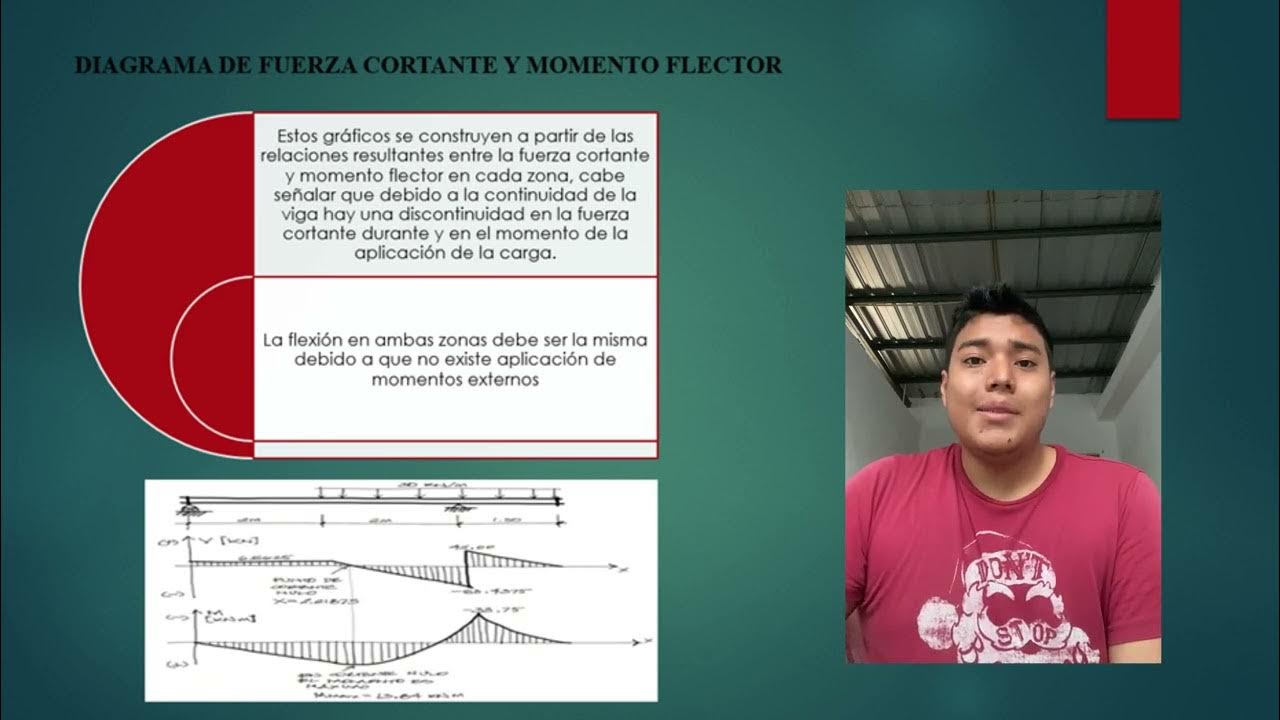
😀 El esfuerzo cortante y el momento de flexión son dos conceptos esenciales para entender cómo se comportan las vigas bajo presión.
😀 El esfuerzo cortante máximo en la viga B1 es de 238.8 kN, y el momento máximo de flexión es de 583.2 kNm, lo que indica cuánta presión y flexión puede soportar sin dañarse.

Q & A

¿Qué son las cargas distribuidas uniformemente y las cargas triangulares en el contexto de los edificios?
-Las **cargas distribuidas uniformemente** se refieren a la distribución de peso de manera pareja sobre una superficie, como el peso de un piso. Las **cargas triangulares**, por otro lado, se refieren a un peso que no se distribuye de manera uniforme, sino que es más pesado en un extremo, formando una forma triangular.
¿Cómo se calcula el peso que puede soportar una viga como la Viga B1?
-Para calcular el peso que puede soportar la viga B1, se multiplican las áreas de las cargas (triangular y rectangular) por una mezcla especial de cargas: 1.4 veces la carga muerta (peso de los materiales) y 1.6 veces la carga viva (peso de personas y muebles). Luego se suman los resultados para obtener el total de peso que la viga puede soportar.
¿Qué es una carga muerta y una carga viva?
-La **carga muerta** es el peso de los materiales permanentes de un edificio, como los materiales de construcción. La **carga viva** incluye el peso de todo lo que puede moverse, como personas, muebles y equipos dentro del edificio.
¿Qué significa 'reacción final' en el contexto de la Viga B2?
-La **reacción final** es el peso adicional que la Viga B2 soporta debido al peso que transfiere la Viga B1. Esto ocurre cuando una viga transfiere parte de su carga a la viga adyacente.
¿Cómo se calcula la fuerza de corte máxima de la Viga B1?
-La fuerza de corte máxima de la Viga B1 se calcula dividiendo la carga total de diseño (4776 kilonewtons) entre dos. Esto nos da 238.9 kilonewtons, que es la fuerza máxima que la viga puede soportar antes de empezar a ceder.
¿Qué es un momento flector y cómo se calcula para la Viga B1?
-El **momento flector** es la cantidad de flexión que una viga puede soportar sin romperse. Para calcularlo, se utiliza la fuerza de corte y las distancias involucradas en el sistema de carga. En el caso de la Viga B1, el momento flector máximo calculado fue de 583.20.
¿Qué implica el término 'carga triangular' y cómo afecta a la viga B1?
-La **carga triangular** es un tipo de carga no uniforme, donde el peso es más pesado en un extremo y se reduce hacia el otro. En el caso de la Viga B1, la carga triangular representa una porción del piso que tiene una distribución de peso desigual, lo que se calcula como un área triangular.
¿Por qué la Viga B2 tiene que soportar más peso que solo su propia carga?
-La Viga B2 tiene que soportar más peso porque también recibe parte del peso de la Viga B1 a través de la **reacción final**. Esto significa que no solo sostiene su propia carga, sino también el peso que le transfiere la Viga B1, trabajando en conjunto.
¿Cómo se determina el tamaño de una carga trapezoidal como la de la Viga B2?
-Para determinar el tamaño de una carga trapezoidal, se suman los lados superior e inferior del trapecio y luego se multiplica por la altura. Esto da el área total, que luego se utiliza para calcular el peso que la viga puede soportar aplicando la fórmula de cargas.
¿Qué importancia tiene el cálculo de fuerzas y momentos en la ingeniería estructural?
-Los cálculos de fuerzas y momentos son fundamentales en la ingeniería estructural porque permiten determinar cuánta carga puede soportar una viga o estructura sin que se deforme o rompa. Estos cálculos garantizan la seguridad de los edificios, asegurando que pueden resistir el peso de los materiales, las personas y otros factores externos.