Time Complexity | Big O Notation | Data Structures & Algorithms | JomaClass

Summary

This video introduces the concept of time complexity, explaining its importance in evaluating the efficiency of algorithms. It covers different types of time complexities such as constant, linear, and quadratic, using examples like searching for a book in lockers. The video highlights the use of Big O notation to generalize algorithm performance regardless of external factors like computer speed. It also delves into asymptotic analysis, emphasizing how coefficients and constants become less significant as input size grows. The video concludes with practical examples to reinforce the understanding of time complexity in algorithm design.

Takeaways

• 😀 Time complexity is a way to express the efficiency of an algorithm as the input size increases, independent of external factors like computer speed.
• 😀 Directly measuring the runtime of an algorithm is not effective because it depends on the size of the input and other hardware factors.
• 😀 Big O notation is used to classify algorithms based on how their runtime grows with the size of the input.
• 😀 O(1) represents constant time complexity, where the algorithm takes the same time to run regardless of input size.
• 😀 O(n) represents linear time complexity, where the runtime grows directly in proportion to the size of the input.
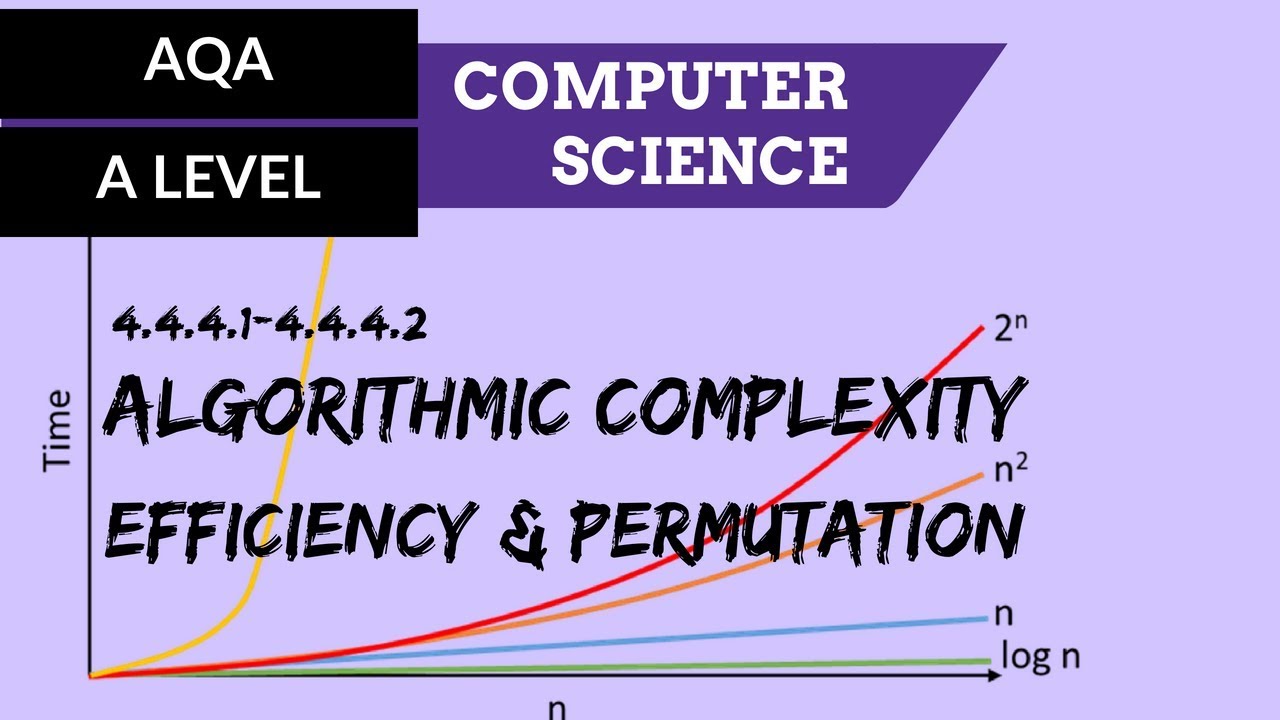
• 😀 O(n²) represents quadratic time complexity, where the runtime grows quadratically with the input size (e.g., nested loops).
• 😀 Asymptotic analysis helps us evaluate algorithms by focusing on their growth rate as input size increases, ignoring factors like hardware.
• 😀 When comparing algorithms with different time complexities, coefficients and constants can be ignored in Big O notation, focusing on the largest growth rate.
• 😀 Algorithms with logarithmic time complexity (O(log n)) are highly efficient, as each iteration reduces the problem size by half.
• 😀 In some cases, an algorithm may seem slower due to external factors (e.g., computer speed), but over time, algorithms with lower time complexity will always perform better as input size increases.

Q & A

What is time complexity, and why is it important?

Time complexity is a way of expressing how fast an algorithm runs as a function of the size of its input. It is important because it provides a standardized way to compare the efficiency of different algorithms, regardless of external factors like computing power or hardware specifications.

Why is measuring the time it takes for an algorithm to run not sufficient for determining its efficiency?

Measuring the actual time an algorithm takes to run isn't sufficient because it depends on various factors like the speed of the computer and the size of the input. For example, the time to process five elements would differ from processing 5,000 elements, so time complexity provides a more generalized way to measure efficiency.

What is Big O notation, and what does it represent?

Big O notation is a mathematical representation used to classify algorithms by how their run time or space requirements grow relative to the size of the input. It provides a way to describe the upper bound of an algorithm's time complexity, focusing on how the algorithm scales as the input size increases.

What is the significance of constant time complexity, O(1)?

Constant time complexity, O(1), means that the time taken by an algorithm is independent of the size of the input. No matter how large the input is, the algorithm will always take the same amount of time to execute, making it highly efficient.

Can an algorithm with a long startup time still be considered O(1)?

Yes, an algorithm can still be considered O(1) even if it has a long startup time, as long as the time taken does not change with the size of the input. The key aspect of O(1) is that the execution time remains constant for any size of the input.

What does linear time complexity, O(n), mean, and how does it relate to input size?

Linear time complexity, O(n), means that the time taken by an algorithm increases linearly with the size of the input. For example, if an algorithm checks each element of an input once, the time taken will be proportional to the number of elements.

What is quadratic time complexity, O(n^2), and when does it occur?

Quadratic time complexity, O(n^2), occurs when an algorithm involves nested loops that each iterate over the input. This means that for every element in the input, the algorithm will loop over the entire input again, resulting in a time complexity that grows quadratically as the input size increases.

How does asymptotic analysis help in comparing algorithms?

Asymptotic analysis helps in comparing algorithms by providing a way to understand how an algorithm performs as the input size grows. It focuses on the behavior of the algorithm for large inputs, ignoring constant factors and lower-order terms to identify which algorithm will eventually perform better as the input size increases.

What happens when we compare algorithms with different time complexities on different computers?

When comparing algorithms on different computers, the performance can be affected by external factors like the computer's speed or processing power. Asymptotic analysis helps to mitigate this issue by focusing on the growth of the algorithm's performance with increasing input size, rather than relying on hardware specifics.

What does dropping non-dominant terms mean when calculating time complexity?

Dropping non-dominant terms means that when calculating time complexity, we disregard terms that grow more slowly than the highest-order term. For example, in an algorithm with O(n^2 + n), we drop the O(n) term because it grows slower than O(n^2), so the overall time complexity is O(n^2).