Angle of Elevation/Angle of Depression Problems
Summary
TLDRIn this video, the focus is on applying right triangle trigonometry to solve real-world problems involving angles of elevation and depression. The instructor explains how to identify these angles, using a horizontal line (horizon) to visualize them. Through examples, such as finding distances from a cliff to a house and calculating building heights across a street, the video demonstrates how to apply trigonometric ratios like tangent. The lessons incorporate key concepts like alternate interior angles, allowing viewers to solve practical problems step by step using trigonometric functions.
Takeaways
- 😀 Angles of depression and elevation are related to the horizontal line (horizon) and involve the observer's line of sight to another point, either below or above their eye level.
- 😀 The angle of depression occurs when looking down, and the angle of elevation occurs when looking up.
- 😀 Both angles (depression and elevation) are congruent when formed by parallel lines and a transversal, thanks to alternate interior angles.
- 😀 A key step in solving problems involving these angles is to always draw a diagram to identify the right triangles and visualize the relationships.
- 😀 In trigonometry problems involving angles of elevation or depression, the tangent ratio (opposite/adjacent) is often used to calculate unknown distances.
- 😀 In the first example, using a 12° angle of depression from the top of a 60-meter cliff, the horizontal distance to a house is calculated to be 282 meters using the tangent ratio.
- 😀 In the second example, two buildings are separated by a 35-meter horizontal distance. The heights of the buildings are determined by breaking the problem into multiple right triangles and using the tangent ratio.
- 😀 When calculating building heights, sometimes multiple right triangles are needed to find unknown distances, like the height of Building B, which is found by combining the height of Building A and an additional calculated distance.
- 😀 The relationship between a given angle, opposite, and adjacent sides is critical to solving these problems using trigonometric ratios, especially with the tangent function.
- 😀 Drawing horizontal lines and identifying angles of elevation and depression from appropriate eye levels is crucial in accurately solving real-world trigonometry problems.
Q & A
What is the definition of an angle of depression?
-An angle of depression is the angle formed by the line of sight from an observer looking down at a point, measured from a horizontal line drawn at the observer's eye level.
What is an angle of elevation?
-An angle of elevation is the angle formed by the line of sight from an observer looking up at a point, measured from a horizontal line drawn at the observer's eye level.
Why are angles of depression and elevation congruent in certain situations?
-Angles of depression and elevation are congruent because they are alternate interior angles formed by parallel lines (such as the horizon and the line of sight) and a transversal (the line of sight from the observer).
How does the angle of depression relate to the right triangle in the cliff example?
-In the cliff example, the angle of depression forms part of the right triangle, allowing the use of trigonometric ratios (like tangent) to calculate the horizontal distance between the observer and the point of interest (the house).
How do you calculate the horizontal distance from the base of the cliff to the house?
-To calculate the horizontal distance, you use the tangent ratio, with the angle of depression (12°) and the vertical height (60m) of the cliff. The formula is tangent of the angle = opposite/adjacent, and solving for the adjacent side gives the distance.
What role does drawing a picture play in solving trigonometry problems?
-Drawing a picture is crucial in trigonometry problems because it helps visualize the situation, allowing for the identification of right triangles and the application of appropriate trigonometric ratios.
In the example with buildings A and B, why is building A considered shorter than building B?
-Building A is considered shorter than building B because the observer on top of building A can look up to see the top of building B, indicating that building A is at a lower elevation compared to building B.
How is the height of building A determined in the example with buildings A and B?
-The height of building A is determined by using the tangent ratio with the angle of depression (34°) and the horizontal distance between the buildings (35m). The tangent of 56° (90° - 34°) is used to calculate the height.
Why are two right triangles used to solve for the height of building B?
-Two right triangles are used to solve for the height of building B because the height consists of two parts: the height of building A and the additional height from building A to the top of building B, requiring the use of separate triangles to calculate each part.
What is the process for finding the total height of building B?
-The total height of building B is found by adding the height of building A (23.6m) to the additional height (15.6m) from the right triangle involving the angle of elevation (24°), giving a total height of 39.2m.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

TRIGONOMETRI (5): PEMBAHASAN SOAL KONTEKSTUAL PERBANDINGAN TRIGONOMETRI ATAU APLIKASI SEHARI-HARI

Trigonometri #14 - Sudut Elevasi dan Sudut Depresi

Manipulating the Trig Ratios in Geometry (example question)
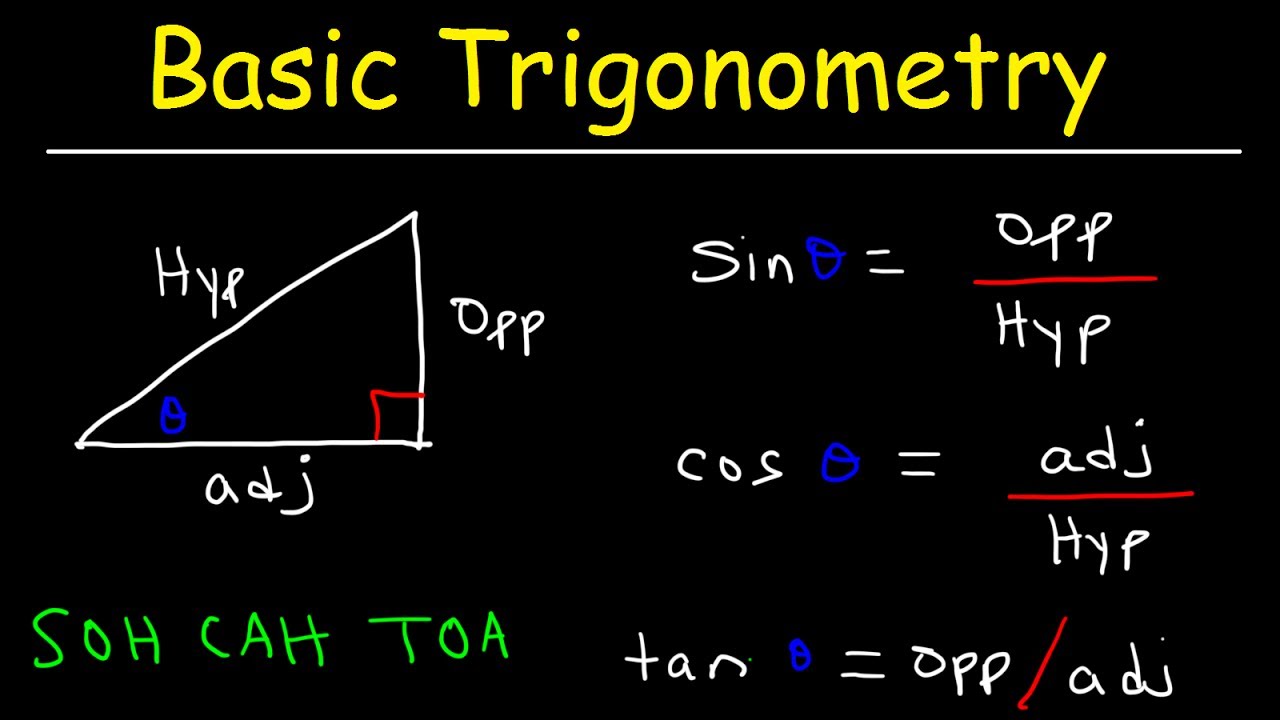
Trigonometry For Beginners!

Perbandingan Trigonometri Part 2- Mengukur Tinggi Benda dengan Clinometer

Aturan Sinus dan Cosinus | Matematika SMA
5.0 / 5 (0 votes)
