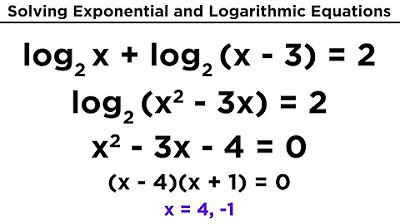Matemática - Aula 13 - Logaritmo - Parte 1

Summary

In this educational video, the host introduces the concept of logarithms, explaining how they simplify solving exponential equations. The video covers the process of solving exponential equations by equating bases, followed by the challenges posed by equations with non-matching bases. The concept of logarithms is introduced to facilitate these calculations, highlighting their applications in various scientific fields such as chemistry, physics, and engineering. The host also discusses the definition of logarithms, basic rules, and examples to clarify their use, ensuring viewers understand the fundamentals before tackling more complex problems.

Takeaways

• 😀 Logarithms were introduced to simplify the calculation of exponential equations, especially when the bases cannot be equalized.
• 😀 Exponential equations can be solved by making the bases equal, but for equations where this isn't possible, logarithms provide an easier solution.
• 😀 The concept of logarithms was developed to assist with complex exponential equations and has applications in fields like chemistry, physics, and engineering.
• 😀 The definition of a logarithm is: log base A of B = X, which means that A raised to the power of X equals B.
• 😀 Logarithms are used to simplify equations where it is difficult to directly equalize the bases of exponential terms.
• 😀 When working with logarithms, the base must be greater than zero and not equal to one, while the argument (logarithm) must also be greater than zero.
• 😀 The number under the logarithmic symbol is called the 'logarithm', the base is the number that defines the logarithmic function, and the result is the exponent.
• 😀 Logarithms help in solving complex equations by converting multiplication and division into addition and subtraction.
• 😀 Logarithmic scales, like the pH scale in chemistry and the Richter scale in seismology, are used to express values that cover a wide range.
• 😀 In practical applications, logarithms are particularly helpful in areas such as cryptography and other engineering processes, where calculations involve exponential growth or decay.

Q & A

What is the main purpose of logarithms as explained in the script?

The main purpose of logarithms, as explained in the script, is to simplify complex calculations in exponential equations, especially when bases cannot be easily equalized.

How do you solve an exponential equation like 2^x = 4?

To solve 2^x = 4, you equalize the bases. Since 4 is 2^2, the equation becomes 2^x = 2^2, which gives x = 2.

Why can't you directly solve 10^x = 2 by equalizing the bases?

You can't directly solve 10^x = 2 by equalizing the bases because there is no simple way to express 2 as a power of 10. Instead, you must approach the problem through approximation or logarithms.

What is the significance of using logarithms in solving exponential equations?

Logarithms are significant in solving exponential equations because they allow you to handle equations where the bases are not easily equalizable, making complex calculations simpler.

What are the applications of logarithms mentioned in the script?

Logarithms have various applications in science, including chemistry (for pH), physics (logarithmic scales), and engineering (cryptography), among others.

What is the definition of a logarithm according to the script?

A logarithm is defined as the inverse of an exponentiation. If log_a(b) = x, then it means a^x = b, where 'a' is the base, 'b' is the logarithmando (the value we are taking the log of), and 'x' is the logarithm.

What are the limitations for the values of the base and the logarithmando in a logarithmic equation?

The base must be greater than 0 and different from 1, and the logarithmando (the value) must also be greater than 0.

In the example log_2(4), why does the answer equal 2?

log_2(4) equals 2 because 2 raised to the power of 2 equals 4 (2^2 = 4).

How do you solve a logarithmic expression like log_2(cube root of 16)?

To solve log_2(cube root of 16), first express 16 as a power of 2, which is 2^4. Then rewrite the cube root as 2^(4/3), so you have 2^x = 2^(4/3). Equalizing the bases gives x = 4/3.

What does the speaker mean by 'cabelo careca' in the context of recognizing powers of 2?

The phrase 'cabelo careca' (bald head) is used informally by the speaker to refer to something that is obvious or easy to recognize, in this case, the fact that 16 is a power of 2 (2^4).