Kekongruenan dan Kesebangunan [Part 3] - Kesebangunan Bangun Datar

Summary

In this educational video, Pak Beni discusses the concept of similarity in planar shapes, focusing on how to determine whether two shapes are similar and how to calculate unknown angles or side lengths. He explains the conditions for similarity, such as equal corresponding angles and proportional corresponding sides. Through examples of photos, Pak Beni demonstrates how to apply these principles, distinguishing similarity from congruence. The video also covers how to solve problems involving similar shapes, including practical exercises for viewers to practice on their own.

Takeaways

• 😀 Two shapes are said to be similar if they have the same shape and proportional side lengths.
• 😀 To determine if two shapes are similar, check if their corresponding angles are equal and if the ratios of their corresponding sides are constant.
• 😀 The example of two photos shows how to check if they are similar by comparing their corresponding sides' ratios.
• 😀 For two shapes to be similar, the ratio of corresponding sides must be the same, even if the sides themselves aren't equal in length.
• 😀 Congruence and similarity share a requirement for equal corresponding angles, but congruence also requires identical side lengths.
• 😀 The symbol for similar shapes is different from that for congruent shapes, indicating their respective relationships.
• 😀 For congruent shapes, all corresponding sides and angles must be identical, while for similar shapes, the corresponding angles are the same, and the sides have equal ratios.
• 😀 In a practical example, when comparing two rectangles, if the side length ratios match, the two rectangles are similar.
• 😀 The lesson emphasizes that congruence guarantees similarity, but similarity doesn't necessarily imply congruence.
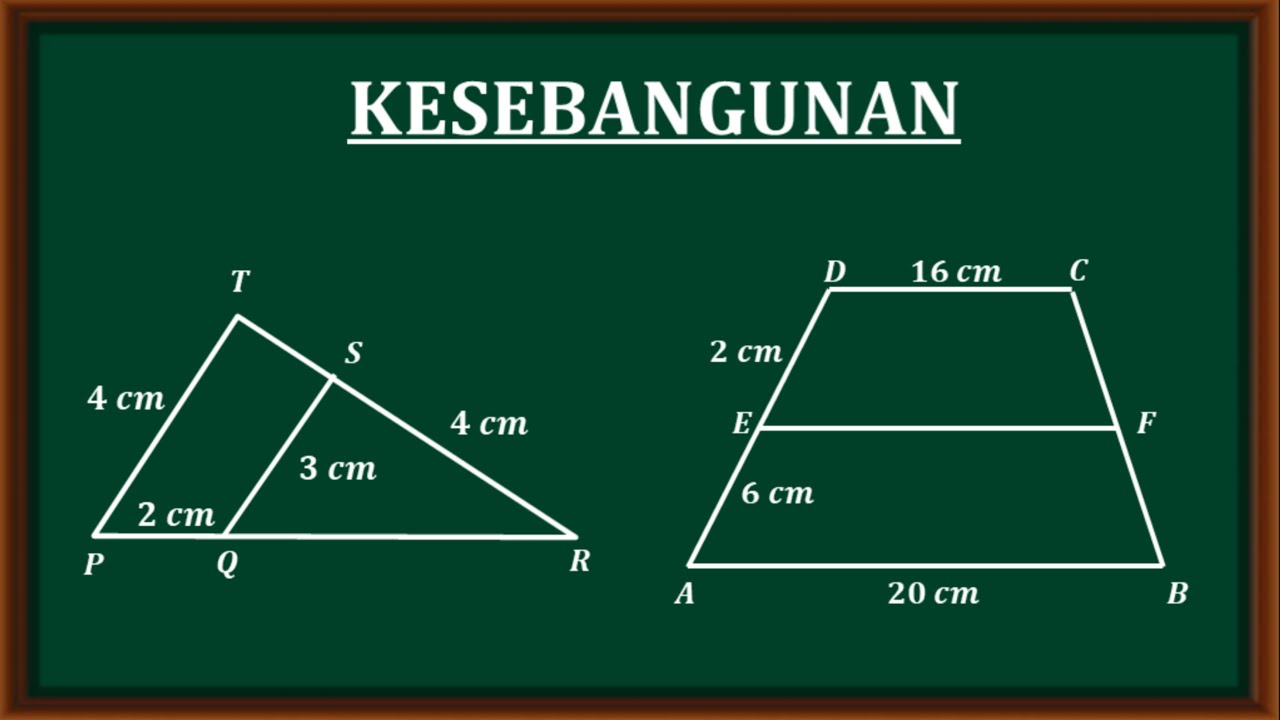
• 😀 The importance of understanding similarity is highlighted through multiple geometric examples, such as comparing trapezoids and solving for unknown lengths using proportions.

Q & A

What is the primary concept discussed in the video?

The video discusses the concept of 'kesebangunan' (similarity) and 'kekongruenan' (congruence) of flat shapes, focusing on how to determine if two shapes are similar or congruent and how to calculate related properties such as side lengths and angles.

How do we determine if two objects are similar?

Two objects are considered similar if they have the same shape. This means their corresponding angles are equal, and the ratio of their corresponding sides must be constant.

What is the difference between 'kesebangunan' (similarity) and 'kekongruenan' (congruence)?

While both concepts involve comparing shapes, the key difference is that in congruence, corresponding sides must be equal in length, while in similarity, the corresponding sides must have the same ratio, but not necessarily equal lengths.

What are the conditions for two shapes to be considered similar?

For two shapes to be considered similar, their corresponding angles must be equal, and the ratio of their corresponding sides must be the same.

How can we determine if two rectangles are similar?

To check if two rectangles are similar, we compare their corresponding angles (which will both be 90° for rectangles) and the ratio of the lengths of corresponding sides. If the ratios are equal, the rectangles are similar.

How do you check if two shapes are congruent?

For two shapes to be congruent, all corresponding sides must be equal in length and all corresponding angles must be equal in measure.

What is the symbol used to denote similarity between two shapes?

The symbol for similarity is '≈' which denotes that two shapes are similar in form but not necessarily identical in size.

What symbol is used to denote two shapes that are not similar?

The symbol used to denote that two shapes are not similar is '≠' which indicates that the shapes do not meet the criteria for similarity.

In the example of two photos, how do we check if they are similar?

We check if the corresponding angles are the same (both are right angles in the case of rectangular photos) and then calculate the ratio of the corresponding sides. If the ratios are the same, the photos are similar.

In the given example, how do we calculate the dimensions of the space left uncovered by a photo on a carton?

The problem states that the photo and the carton are similar. By using the ratio of the photo's width to the carton’s width, and the length of the photo to the carton’s length, we can calculate the uncovered width by subtracting the known photo dimensions from the carton’s dimensions.