OpenCV Python Fourier Transform

Summary

This video explains the concept of Fourier Transform (FT) and its application in image processing using OpenCV and Python. It covers how FT transforms a 2D image from the time domain to the frequency domain, offering benefits like filtering and data compression. Through coding examples, viewers learn to apply Discrete Fourier Transform (DFT), shift low-frequency signals to the center, and use a low-pass filter to compress the image. The video also demonstrates Gaussian and Laplacian filters as low and high-pass filters, respectively, showing how they affect image processing.

Takeaways

• 😀 Fourier Transform converts a 2D image from the time domain to the frequency domain, enabling image processing techniques such as filtering and compression.
• 😀 The Fourier Transform is a mathematical method that expresses any signal as a combination of sine and cosine functions.
• 😀 In image processing, the frequency domain represents various frequency components of the image, while the time domain represents its pixel data.
• 😀 One key application of the Fourier Transform is filtering, where you can apply operations in the frequency domain before converting the image back to the time domain.
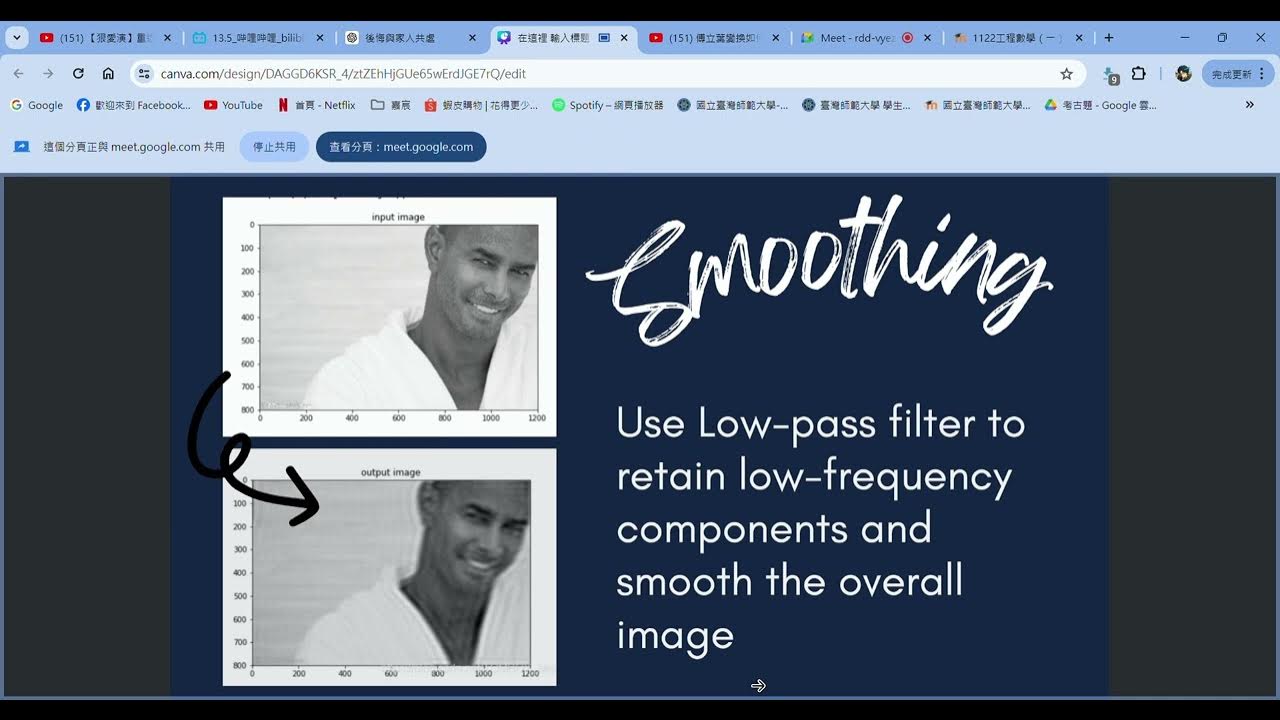
• 😀 Low-pass filtering can be achieved in the frequency domain by masking high-frequency components, allowing you to blur or compress images.
• 😀 Applying Fourier Transform to an image in OpenCV involves using the 'cv2.dft' function and the conversion of the result to decibels for better visibility of frequency components.
• 😀 The Fourier Transform outputs complex numbers, representing both real and imaginary components, which are visualized in the frequency domain after processing.
• 😀 The inverse Fourier Transform (IDFT) allows you to revert the frequency-domain image back to the time domain after manipulating its frequency components.
• 😀 To make frequency-domain images easier to interpret, the FFT shift function is used to reposition low-frequency components to the center of the image.
• 😀 Gaussian and Laplacian filters can be understood as low-pass and high-pass filters, respectively. Gaussian filters emphasize low frequencies, while Laplacian filters highlight high frequencies in an image.

Q & A

What is the Fourier Transform, and why is it important in image processing?

The Fourier Transform is a mathematical technique that converts a 2D image from the time domain to the frequency domain. It is important because it allows for operations like filtering and data compression, enabling manipulation of images based on their frequency components.

What does the frequency domain representation of an image look like?

In the frequency domain, the image is represented in terms of its frequency components. This transformation highlights the frequency content of the image, such as edges and repetitive patterns, which might not be visible in the spatial domain.

How does the Fourier Transform work with respect to image processing?

The Fourier Transform works by breaking down an image into a combination of cosine and sine waves (or exponential functions). This results in a set of frequency coefficients that represent the image in the frequency domain, which can then be manipulated for various tasks like filtering.

What is the purpose of using the DFT (Discrete Fourier Transform) in OpenCV?

The DFT in OpenCV is used to perform the Fourier Transform on images, converting them into the frequency domain. This allows for various frequency-domain operations such as filtering and analysis, which can be very useful in tasks like noise reduction or compression.

Why is the FFT shift function used in Fourier Transform operations?

The FFT shift function is used to shift the low-frequency components to the center of the image. This is done because in the raw frequency domain output, low frequencies are typically located at the edges, making it harder to interpret the results.

What is the effect of applying a low-pass filter in the frequency domain?

Applying a low-pass filter in the frequency domain removes high-frequency components and keeps only the low-frequency components. This results in a blurred or smoothed image, effectively filtering out high-frequency noise and details.

How can image compression be achieved through the Fourier Transform?

Image compression is achieved by retaining only the essential low-frequency components after applying a low-pass filter. These components represent the majority of the image's content, while the high-frequency components (which are often less noticeable) can be discarded, reducing the amount of data required to represent the image.

What is the significance of using decibel scale when plotting Fourier Transformed images?

Using the decibel scale helps to attenuate large values and enhance smaller ones, making the frequency components easier to visualize and analyze. It helps in comparing relative differences in magnitude, especially when the image contains a wide range of frequencies.

What are the characteristics of Gaussian and Laplacian filters in image processing?

The Gaussian filter is a low-pass filter, which keeps low-frequency components and smooths the image, making it appear blurred. The Laplacian filter, on the other hand, is a high-pass filter, emphasizing high-frequency components and edges, making the image appear sharper.

How do you interpret the results of the Gaussian and Laplacian filters based on their Fourier Transforms?

In the Fourier Transform, the Gaussian filter will appear bright at the center, representing low frequencies, while the Laplacian filter will show bright regions at the edges, indicating high frequencies. This highlights the role of each filter as a low-pass and high-pass filter, respectively.