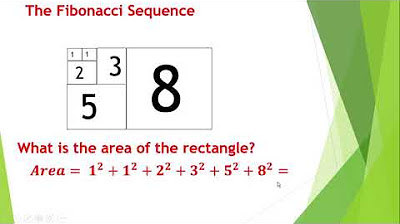The Beauty of Mathematics | Mathematics Motivational Video

Summary

In this lecture, the speaker delves into the world of mathematics, emphasizing the infinite patterns that exist in nature and their relationship with art and truth. With references to advanced concepts like Fourier systems and natural logarithms, the speaker passionately argues that mathematical formulas are not inventions but discoveries. The speaker also alludes to the profound connection between mathematics and the infinite, drawing parallels with the creative genius of Mozart. The ultimate message is that mathematics is a pursuit of absolute perfection, a truth reflected in the world around us.

Takeaways

• 😀 There are over 159 quintillion (159 with 18 zeros) possible settings for the plug board cables.
• 😀 Patterns exist everywhere, from colors and light to mathematical reflections, revealing themselves in complex forms.
• 😀 The speaker has placed an advanced Fourier system on a chalkboard, hoping someone will prove it by the end of the semester.
• 😀 The first person to prove the system will gain both the speaker's favor and potential fame and fortune.
• 😀 The concept of 'truth' is explored through mathematics, where formulas exist and are discovered, not invented.
• 😀 The speaker compares mathematics to art, where it reflects truth, which is likened to a personal belief or church.
• 😀 Like Mozart could hear a symphony in his head, mathematicians can 'dance with numbers to infinity' in pursuit of perfection.
• 😀 The mathematical formulas and systems discussed already exist in nature and can be revealed through exploration.
• 😀 An example formula is provided: natural log of constant multiplied by x equals the natural log of one plus b squared.
• 😀 The speaker hints at a critical and possibly controversial view on the future of Prussian mathematics, subtly critiquing its limitations.

Q & A

What is the significance of '159 with eighteen zeros behind it' in the transcript?

The phrase refers to the number of possible settings of a plug board, which is over 150 million million million, or exactly 159 with eighteen zeros. It emphasizes the vast scale and complexity of the system being discussed.

What does the speaker mean by 'there are patterns in everything'?

The speaker is highlighting the idea that patterns exist in various forms throughout nature, mathematics, and life in general. These patterns are fundamental to understanding the world, as they can be observed in phenomena like color, light, and water reflections.

How does the speaker relate math to art in this transcript?

The speaker draws a parallel between mathematics and art, claiming that both reveal truths and reflect a higher form of understanding. Just as music or visual art can express profound truths, math, in its complexity and beauty, mirrors these same principles.

What is the significance of the 'advanced Fourier system' mentioned in the transcript?

The advanced Fourier system on the chalkboard represents a complex mathematical tool that can decompose functions or signals into their constituent frequencies. The speaker seems to be encouraging students to explore this system, which is crucial in many scientific fields, including signal processing and wave analysis.

What does the speaker mean by 'explorers of infinity'?

The phrase suggests that mathematicians, like explorers, venture into the boundless world of mathematical concepts, constantly searching for deeper understanding and striving toward absolute perfection, especially in their study of infinite or idealized forms.

How does the speaker view mathematical formulas in the transcript?

The speaker believes that mathematical formulas do not originate from human invention, but rather, they already exist in nature. Mathematicians merely discover these truths, akin to uncovering a pre-existing order in the universe.

What is the connection between Aristotle and the mathematical formula provided?

The speaker refers to Aristotle as an example of someone who could benefit from understanding modern mathematics, suggesting that even classical thinkers like Aristotle would find relevance in current mathematical principles, such as the natural log function and its application in formulas.

Why does the speaker mention Mozart in relation to mathematics?

The comparison to Mozart suggests that just as Mozart could hear an entire symphony in his head, mathematicians can visualize or intuitively grasp complex mathematical concepts, reflecting the idea of a deeply ingrained and instinctive understanding of their craft.

What does the speaker mean by saying 'we do not invent these formulas, they already exist'?

The speaker is emphasizing a philosophical perspective on mathematics, asserting that mathematical truths are not human creations, but rather discoveries of universal principles that have always existed, waiting to be uncovered.

How does the speaker's view of mathematics reflect a deeper truth or purpose?

The speaker views mathematics as a path to uncovering deeper, universal truths. This reflects a belief that mathematics is not merely a tool for calculation, but a form of exploration and discovery that brings us closer to understanding the fundamental nature of reality.