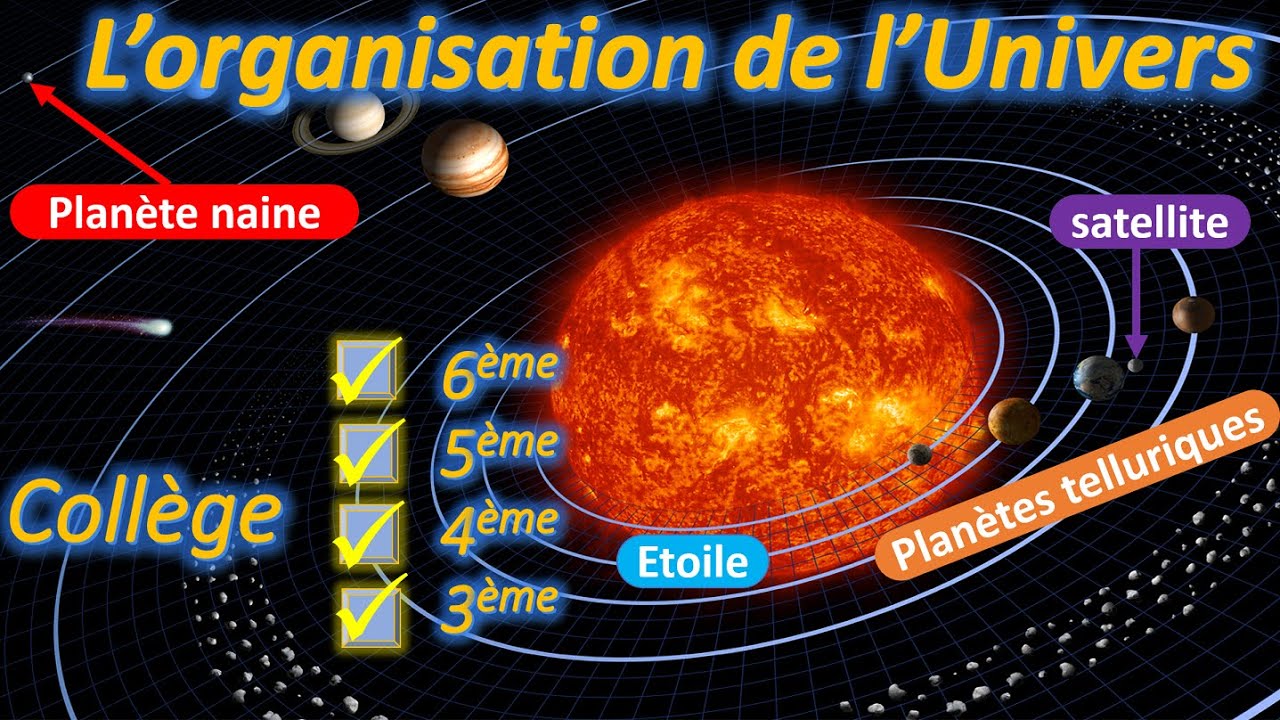
Mouvement des satellites et des planètes - physique chimie terminale
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
什么是弗雷内坐标系?
-弗雷内坐标系是一种随物体运动的坐标系,它的原点始终与物体相结合。这个坐标系有两个正交的单位向量:一个是切向量(t),与物体的运动轨迹切线方向一致;另一个是法向量(N),指向运动轨迹的中心。该坐标系用于简化物体运动分析,尤其在处理圆形轨道时更为有效。
为什么传统的笛卡尔坐标系在处理卫星轨道时不适用?
-笛卡尔坐标系在处理卫星轨道时,涉及的加速度和速度的计算会非常复杂,特别是需要大量的三角函数计算。使用弗雷内坐标系能够简化这些计算,避免繁琐的三角函数,从而使方程更简单、更易于操作。
如何通过牛顿第二定律推导卫星的加速度?
-根据牛顿第二定律,卫星所受的重力加速度等于地球对卫星的引力。此引力表达式为F = G * (M_s * M_T) / r^2,其中G是引力常数,M_s和M_T分别是卫星和地球的质量,r是卫星与地球之间的距离。通过这个式子,可以得出卫星的加速度表达式:a = G * M_T / r^2。
什么是卫星的轨道周期?
-卫星的轨道周期是卫星绕地球一圈所需的时间。在圆形轨道上,周期T与轨道半径r之间存在一个关系式:T = 2πr / v,其中v是卫星的轨道速度。周期与轨道半径和卫星的速度密切相关。
如何从速度表达式推导开普勒第三定律?
-通过将速度表达式v = 2πr / T代入牛顿引力公式,可以得到T² / r³ = 常数。这个常数由地球的质量和引力常数决定,因此对于任何绕地球运动的物体来说,T² / r³都是一个常数,这就是开普勒的第三定律。
开普勒第三定律的数学公式是什么?
-开普勒的第三定律的数学公式是T² / r³ = 常数,其中T是轨道周期,r是轨道半径。这个常数与地球的质量和引力常数相关,因此对于绕地球运动的任何物体,T² / r³都是一个固定的常数。
什么是静止卫星轨道?
-静止卫星轨道是一种特殊的轨道,其中卫星与地球表面的某一固定点保持相对静止。这种轨道只能位于赤道上,且卫星的轨道周期必须与地球自转周期相同,通常约为23小时56分钟。
如何计算卫星的静止轨道高度?
-静止卫星的轨道高度可以通过开普勒第三定律推导出来。首先,通过已知的地球质量、引力常数和地球自转周期,计算出静止卫星的轨道半径r,然后从该半径中减去地球的半径,就能得到卫星的高度。计算结果通常为约36,000公里。
为什么地球的自转周期不是准确的24小时?
-地球的自转周期略短于24小时,约为23小时56分钟,这被称为恒星日。这个差异是由于地球绕太阳的公转运动所导致的,因此地球自转一周的实际时间稍短于24小时。
为什么在计算静止卫星轨道时需要考虑单位的转换?
-在进行静止卫星轨道计算时,需要确保所有物理量(如地球半径、卫星轨道半径、引力常数等)都使用相同的单位系统。通常,我们需要将单位统一为国际单位制(米、秒等),以确保计算结果的准确性。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)