How to Solve ANY Related Rates Problem [Calc 1]
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
什么是相关速率问题的步骤流程?
-相关速率问题的步骤流程包括:1) 画出两个图;2) 明确问题的目标;3) 从泛化图中写出一个方程,将所有变量关联起来;4) 对方程进行微分;5) 在给定的瞬间评估该方程;6) 解出并得到目标变量。
在相关速率问题中,泛化图和瞬时图的区别是什么?
-泛化图代表了问题的普遍情况,适用于所有时刻,标出所有已知的变量和常数;而瞬时图代表了某一特定时刻的情况,通常需要根据问题的具体条件进行补充或修改。
如何在相关速率问题中表示流量单位?
-流量单位通常表示为体积变化率,即单位时间内的体积变化,符号为dV/dt。例如,在给定问题中,水流入的速率是2立方米/分钟,表示为dV/dt = 2。
如何通过立方体体积公式关联变量?
-对于一个圆柱体,体积V = πr²h,其中r是常数(例如4米),h是随时间变化的变量。通过这种方式,可以将体积与高度h关联起来,得到V = 16πh。
为什么需要在相关速率问题中对方程进行微分?
-对方程进行微分是为了得到涉及时间变化的方程,从而能够找到与时间相关的变量速率。通过微分,可以得到类似于dV/dt和dh/dt的关系,这有助于解决问题中的目标。
如何评估微分方程并解出目标变量?
-在评估微分方程时,需要根据瞬时图中的数据来替换变量值,例如已知的流量dV/dt,或者通过几何关系得到的其它参数。评估后可以通过代数操作解出目标变量,例如求得dh/dt,即水位变化速率。
在求解过程中,如何处理圆锥形相关速率问题与圆柱形问题的不同?
-圆锥形问题与圆柱形问题的不同在于,圆锥的半径r是与高度h相关的,因此需要在方程中加入r与h之间的关系,而圆柱体的半径是常数,因此方程较为简单。
在更复杂的相关速率问题中,如何确定合适的方程?
-在更复杂的相关速率问题中,需要通过分析问题的几何关系和目标变量的变化,确定合适的方程。通常会使用三角函数或几何关系来将不同变量关联起来,例如使用正切函数tan(θ)来关联角度和距离。
为什么需要使用三角函数来解决相关速率问题中的某些几何问题?
-使用三角函数(如正切、余弦或正弦)是因为相关速率问题中涉及的常常是直角三角形,三角函数能够有效地将角度、边长和时间变化速率联系起来。例如,tan(θ) = x/80可以帮助我们将角度与距离关联起来。
在处理与跑步者相关的相关速率问题时,如何确定目标速率?
-在处理与跑步者相关的相关速率问题时,目标速率通常是指光束旋转的角速度dθ/dt。通过分析光束与跑步者之间的几何关系,使用合适的方程(如正切关系)进行微分并求解该速率。
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Problem Solving using Polya's 4 step method|Tano, Arjyll B.

PDE : Aplikasi Sistem Persamaan Diferensial Linear OrdeSatu Di Bidang Kimia Masalah Pencampuran
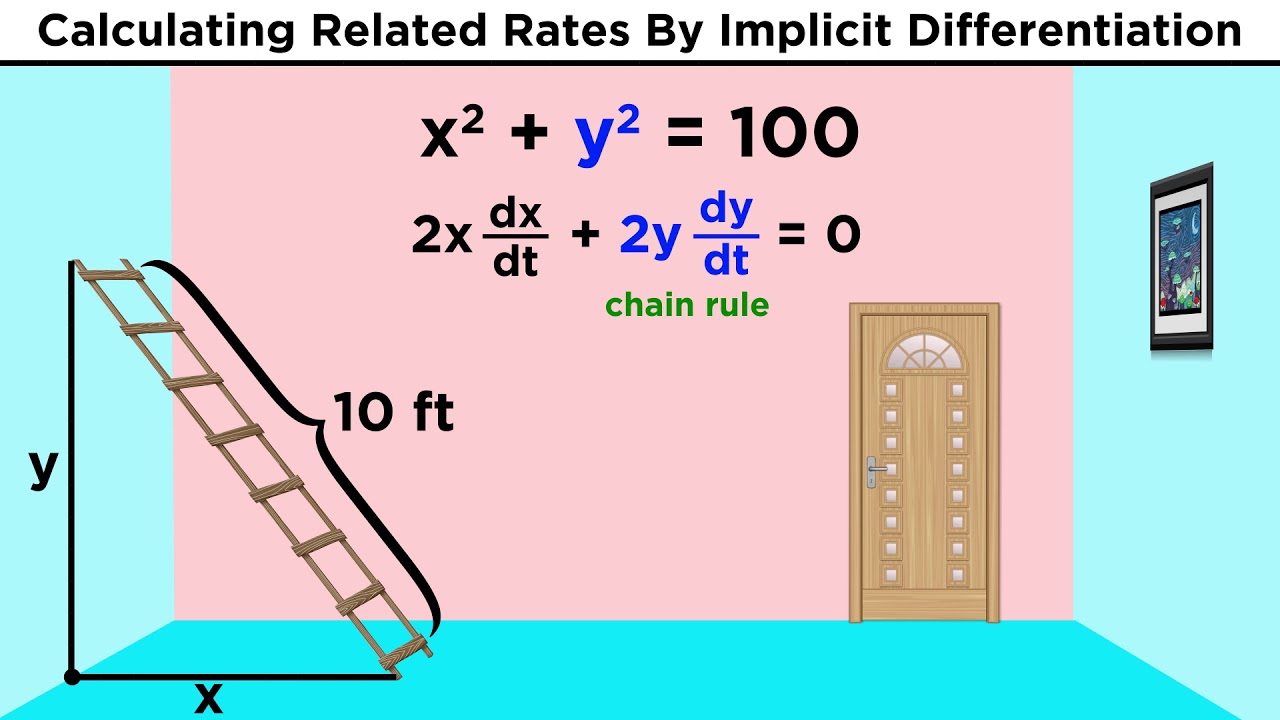
Related Rates in Calculus

Introduction to Related Rates

時計算の基本【中学受験・SPI・公務員試験対策】(時計算1基本編)

Implicit differentiation, what's going on here? | Chapter 6, Essence of calculus

Related Rates - Inflated Balloon & Melting Snowball Problem - Surface Area & Volume
5.0 / 5 (0 votes)